Introduction:

This tutorial goes over the basics of linear algebra, which is a very important concept in computer graphics.

Vectors:

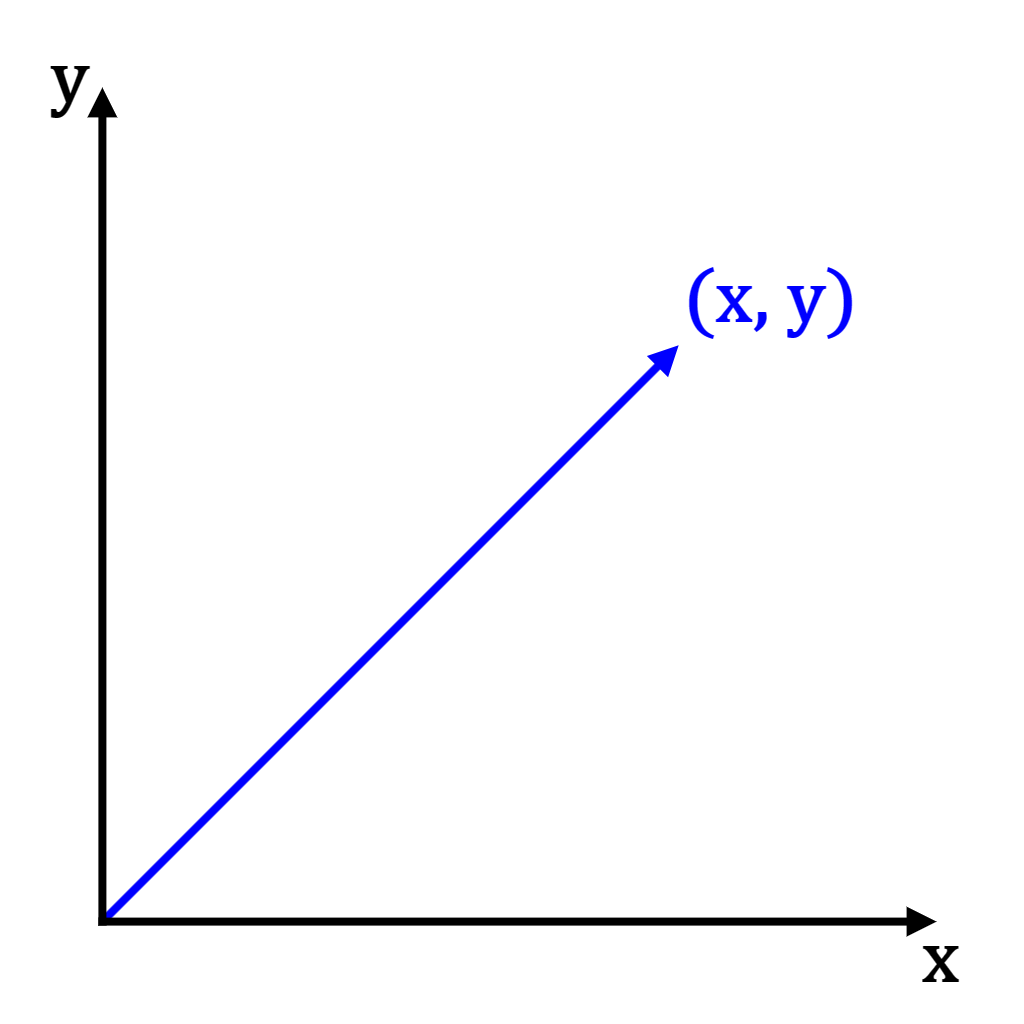
Vectors are numbers, or pairs of numbers, which have a length and direction. The overhead arrow,

\to

, is common notation for vector variables (i.e.

\vec{a}

). Vectors are commonly expressed as coordinates, for example a 3D vector

\vec{v}

is equivalent to the 3D coordinates

(x, y, z)

.

In computer graphics, a vector are used for many different things, a few examples would be:

Points of a 3D model
Position of a character or object
Direction a character or object is moving in

Vector Operations:

Vector length:

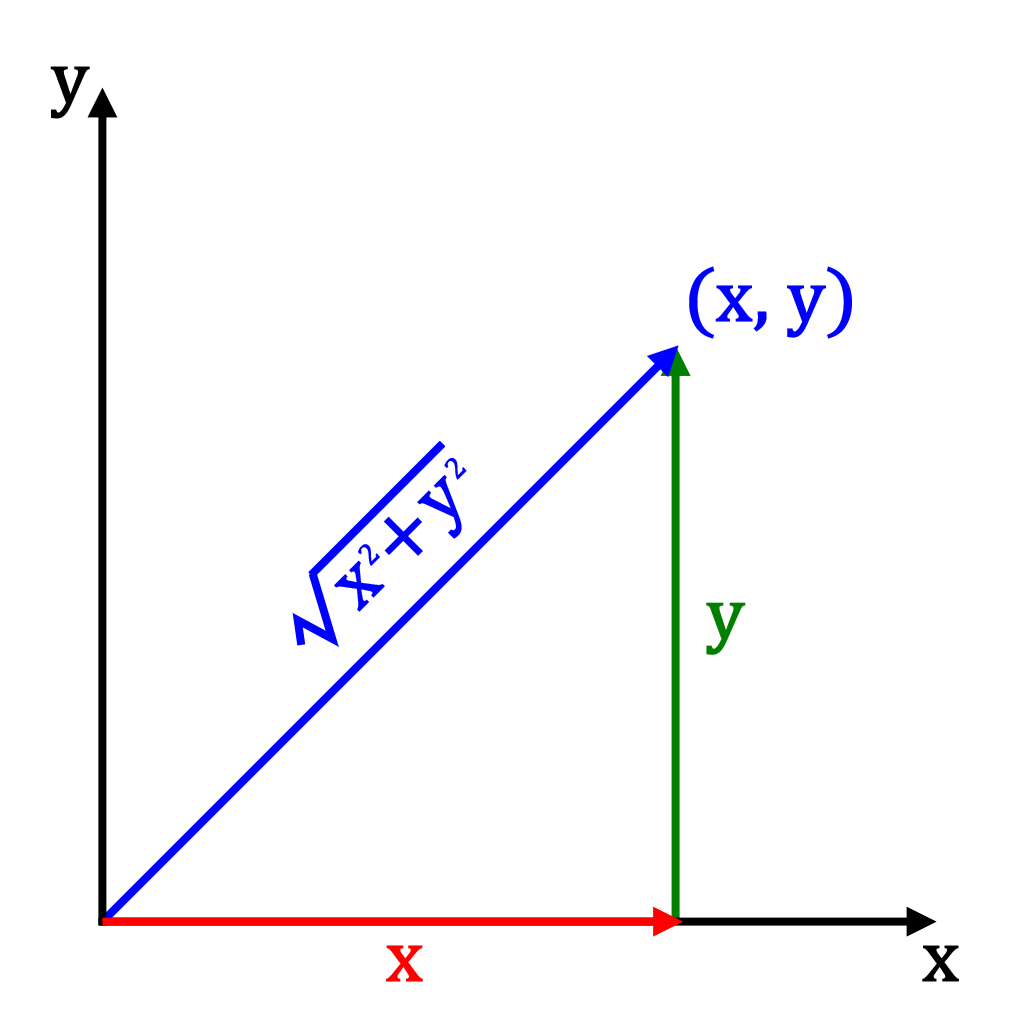
A vector's length, denoted by 2 vertical bars

||

, can be calculated using Pythagorean's theorem. For instance, the length of a 2D vector

\vec{v} = (x, y)

is

|| \vec{v} || = \sqrt{x^{2} + y^{2}}

. In 3D, this would be:

\vec{v} = (x, y, z)

|| \vec{v} || = \sqrt{x^{2} + y^{2} + z^{2}}

A vector which has length 1 is called a unit vector. Unit vectors have many useful properties, including:

Ideal for storing directions
Easy to scale to any length (by multiplying with a scalar, covered next)

Scalar multiplication:

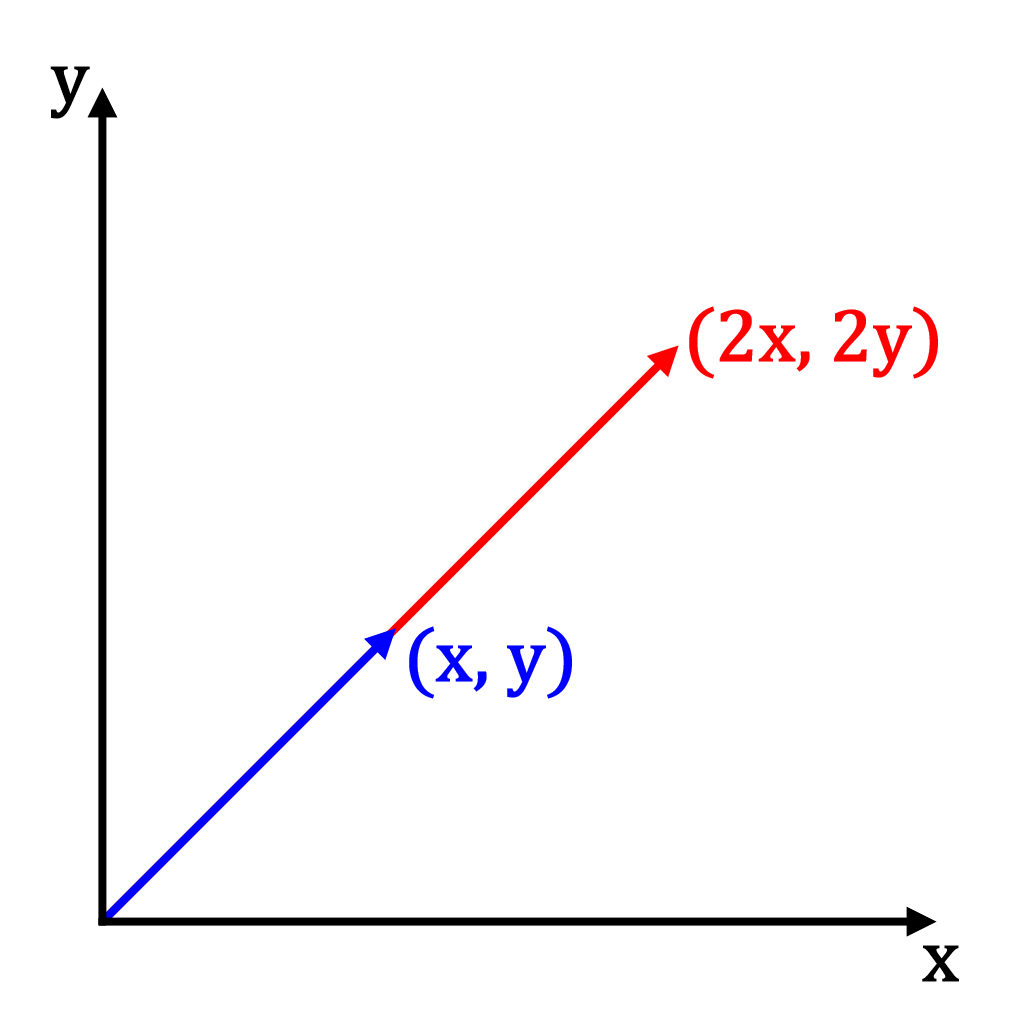
Scalar multiplication multiplies a vector's elements by a scalar value, which essientially scales a vector's length. In the 3D case, this is:

s \cdot \vec{v}

= s \cdot (x, y, z)

= (s \cdot x, s \cdot y, s \cdot z)

For example, multiplying the 2D vector

\vec{v} = (2, 3)

by the scalar value

4

gives:

4 \cdot (2, 3)

= (4 \cdot 2, 4 \cdot 3)

= (8, 12)

If a vector is a unit vector and it gets multiplied by a scalar value, its length will become equal to that scalar value:

|| \vec{v} || = 1

\Rightarrow s \cdot || \vec{v} || = s \cdot 1

\Rightarrow || s \cdot \vec{v} || = s

Vector addition:

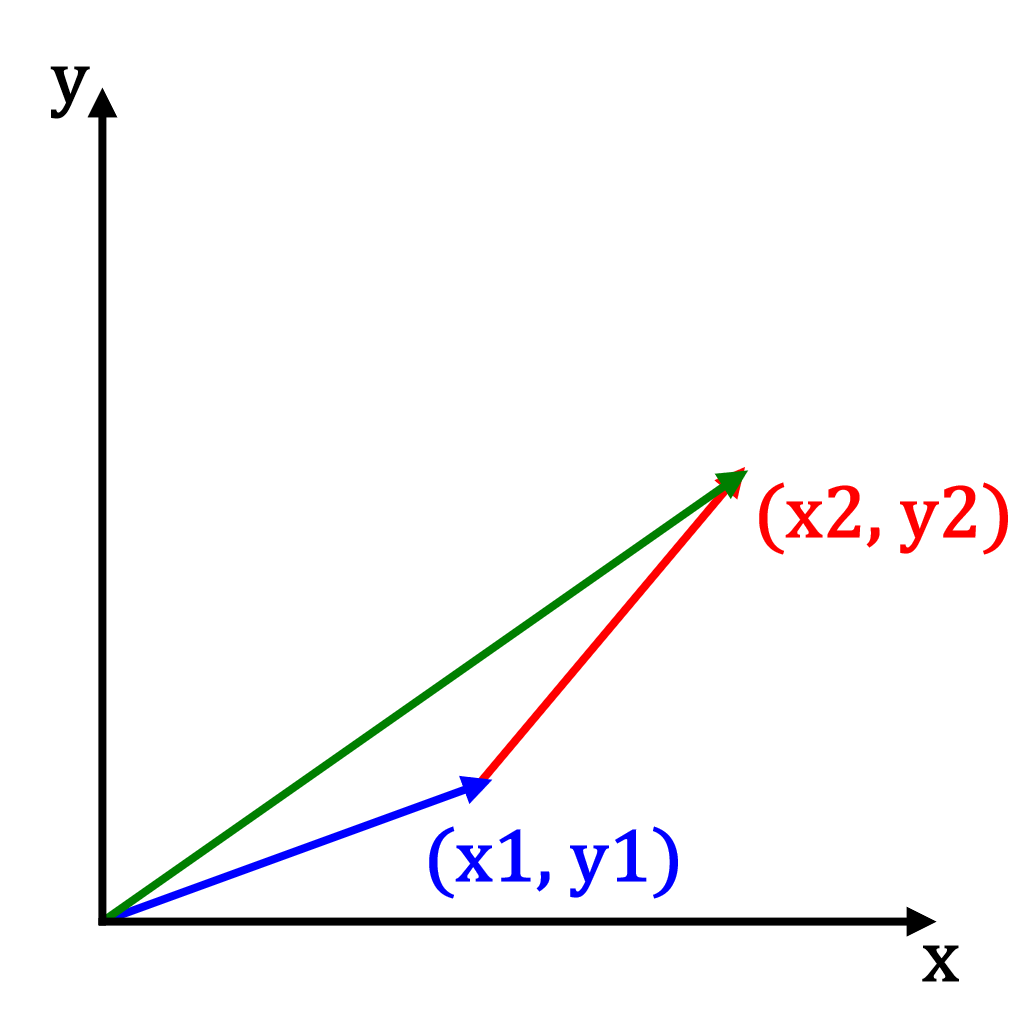
Vectors can be added together to produce new vectors. Vector addition simply adds each vectors element's together, for example in 3D that is:

{\vec{v}}_{1} + {\vec{v}}_{2}

= (x_{1}, y_{1}, z_{1}) + (x_{2}, y_{2}, z_{2})

= (x_{1} + x_{2}, y_{1} + y_{2}, z_{1} + z_{2})

Vector addition is commutative, so the order of addition does not matter.

An example of somewhere vector addition may be useful is moving objects around a 3D world, an offset vector can be added to the object's current position to move it around.

Vector subtraction:

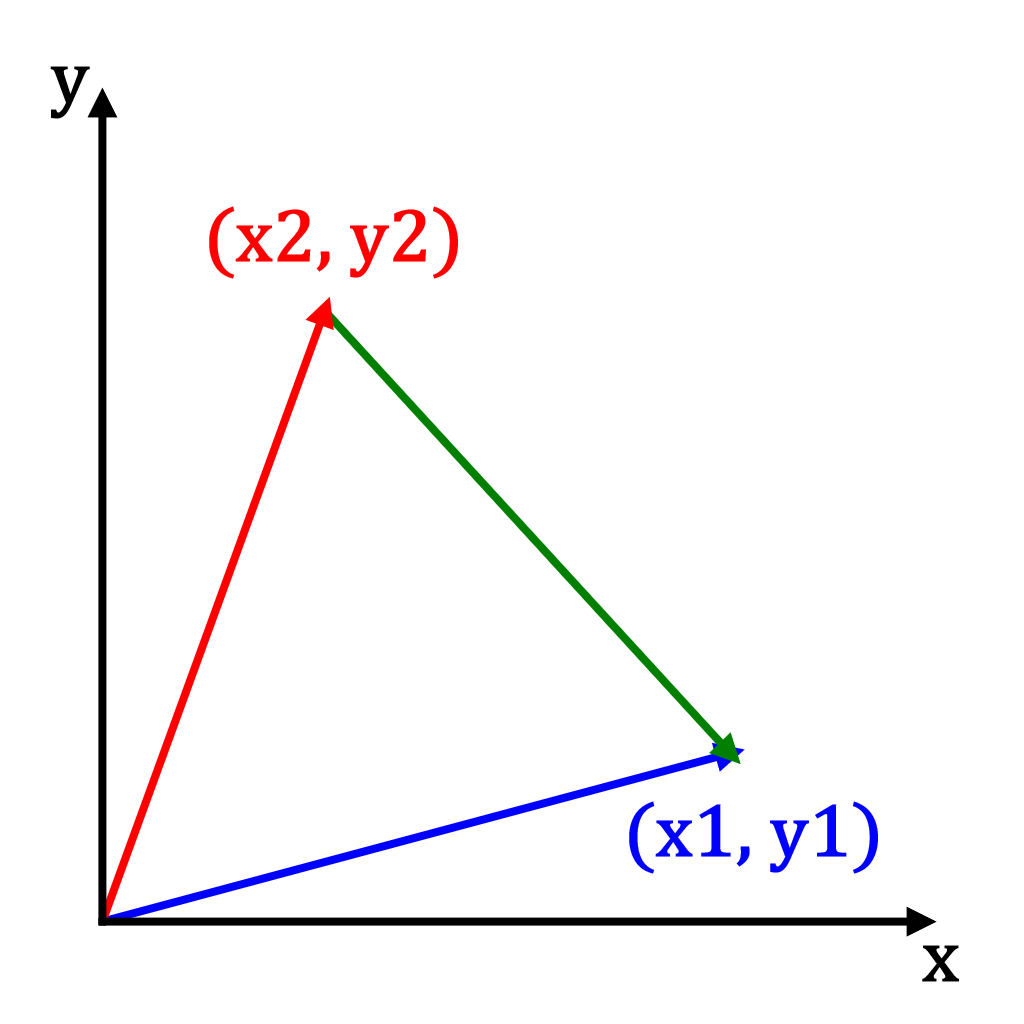
Vectors can subtracted to calculate the differences between vectors. Vector subtraction simply subtracts each vector's elements, for example in 3D that is:

{\vec{v}}_{1} - {\vec{v}}_{2}

= (x_{1}, y_{1}, z_{1}) - (x_{2}, y_{2}, z_{2})

= (x_{1} - x_{2}, y_{1} - y_{2}, z_{1} - z_{2})

An example of somewhere vector subtraction may be useful is calculating a difference vector between 2 objects, or calculating directions between objects, etc.

Vector dot product:

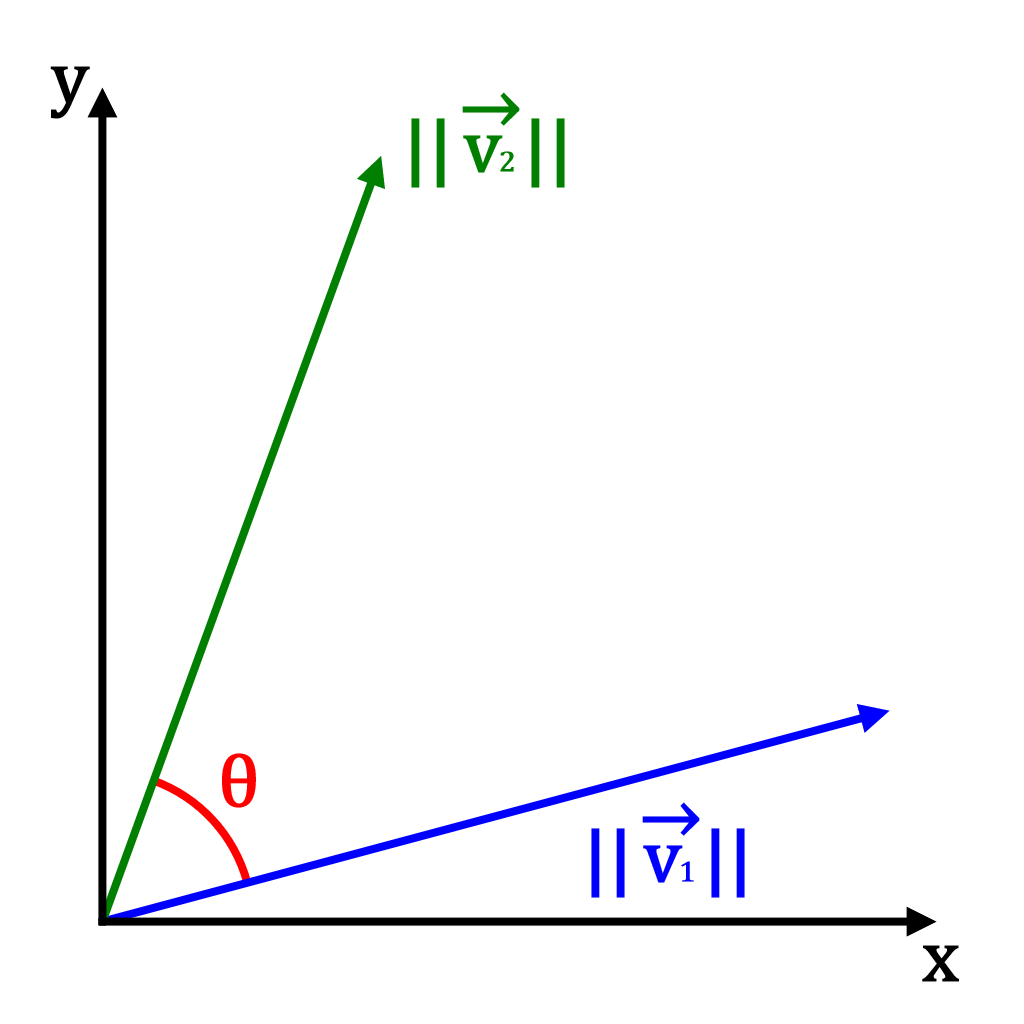
The dot product, denoted by "

\cdot

", of two vectors is a very important and common operation. The dot product of two 3D vectors is calculated as follows:

{\vec{v}}_{1} \cdot {\vec{v}}_{2} = (x_{1} \cdot x_{2}) + (y_{1} \cdot y_{2}) + (z_{1} \cdot z_{2})

This calculation can be generalized to any number of dimensions (2D, 4D, etc.).

This calculation is equivalent to:

{\vec{v}}_{1} \cdot {\vec{v}}_{2} = || {\vec{v}}_{1} || \cdot || {\vec{v}}_{2} || \cdot \cos (θ)

Note that

θ

is the angle between

{\vec{v}}_{1}

and

{\vec{v}}_{2}

.

The

\cos (θ)

makes the dot product very useful to find the angle between two vectors using

arccosine

:

{\vec{v}}_{1} \cdot {\vec{v}}_{2} = || {\vec{v}}_{1} || \cdot || {\vec{v}}_{2} || \cdot \cos (θ)

\frac{{\vec{v}}_{1} \cdot {\vec{v}}_{2}}{|| {\vec{v}}_{1} || \cdot || {\vec{v}}_{2} ||} = \cos (θ)

\Rightarrow θ = arccosine (\frac{{\vec{v}}_{1} \cdot {\vec{v}}_{2}}{|| {\vec{v}}_{1} || \cdot || {\vec{v}}_{2} ||})

Note: If

{\vec{v}}_{1}

and

{\vec{v}}_{2}

are unit vectors, there is no need divide by

|| {\vec{v}}_{1} || \cdot || {\vec{v}}_{2} ||

.

Another very useful property of the dot product is that if it is zero, it means the two vectors are perpendicular:

{\vec{v}}_{1} \cdot {\vec{v}}_{2} = (x_{1} \cdot x_{2}) + (y_{1} \cdot y_{2}) + (z_{1} \cdot z_{2}) = 0

\Rightarrow || {\vec{v}}_{1} || \cdot || {\vec{v}}_{2} || \cdot \cos (θ) = 0

\Rightarrow \cos (θ) = 0

\Rightarrow θ = \frac{π}{2} or θ = \frac{3 π}{2}

Also note that a vectors dot product with itself is its length squared:

\vec{v} \cdot \vec{v}

= x \cdot x + y \cdot y + z \cdot z

= x^{2} + y^{2} + z^{2}

Vector cross product:

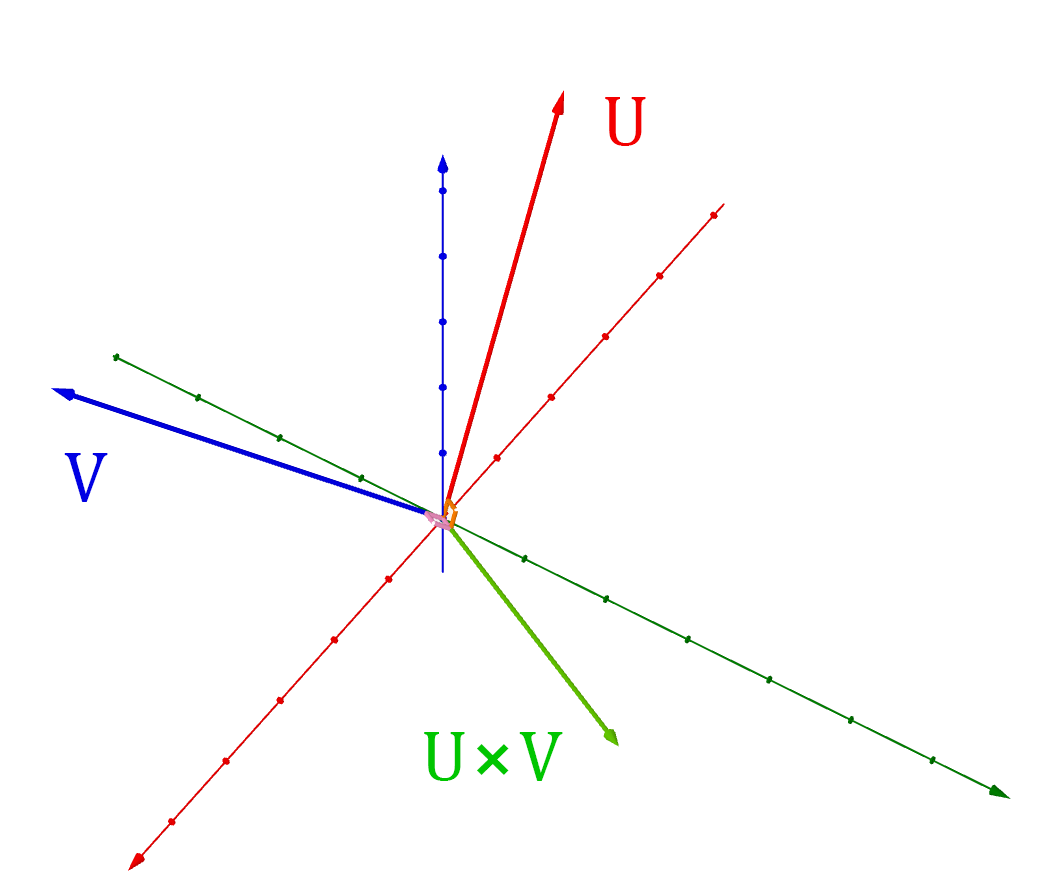
The cross product, denoted by "

\times

", of two vectors is another very common and important operation. The cross product can only be computed on 3D vectors, and the calculation is the following matrix determinant:

\vec{u} \times \vec{v} = (u_{y} v_{z} - u_{z} v_{y}) i - (u_{x} v_{z} - u_{z} v_{x}) j + (u_{x} v_{y} - u_{y} v_{x}) k

This is equivalent to the determinant of the matrix (covered in next matrix section):

\vec{u} \times \vec{v} = | \begin{matrix} i & j & k \\ u_{x} & u_{y} & u_{z} \\ v_{x} & v_{y} & v_{z} \end{matrix} |

This cross product calculation is equivalent to:

\vec{u} \times \vec{v} = || \vec{u} || \cdot || \vec{v} || \cdot \sin (θ) \vec{n}

Note that

θ

is is the angle between

\vec{u}

and

\vec{v}

, and

\vec{n}

is the vector perpendicular to both

\vec{u}

and

\vec{v}

. This means the cross product returns a new vector which is perpendicular to both

\vec{u}

and

\vec{v}

.

The cross product can be very useful for many operations, i.e. calculating surface normals for lighting.

Vector projection:

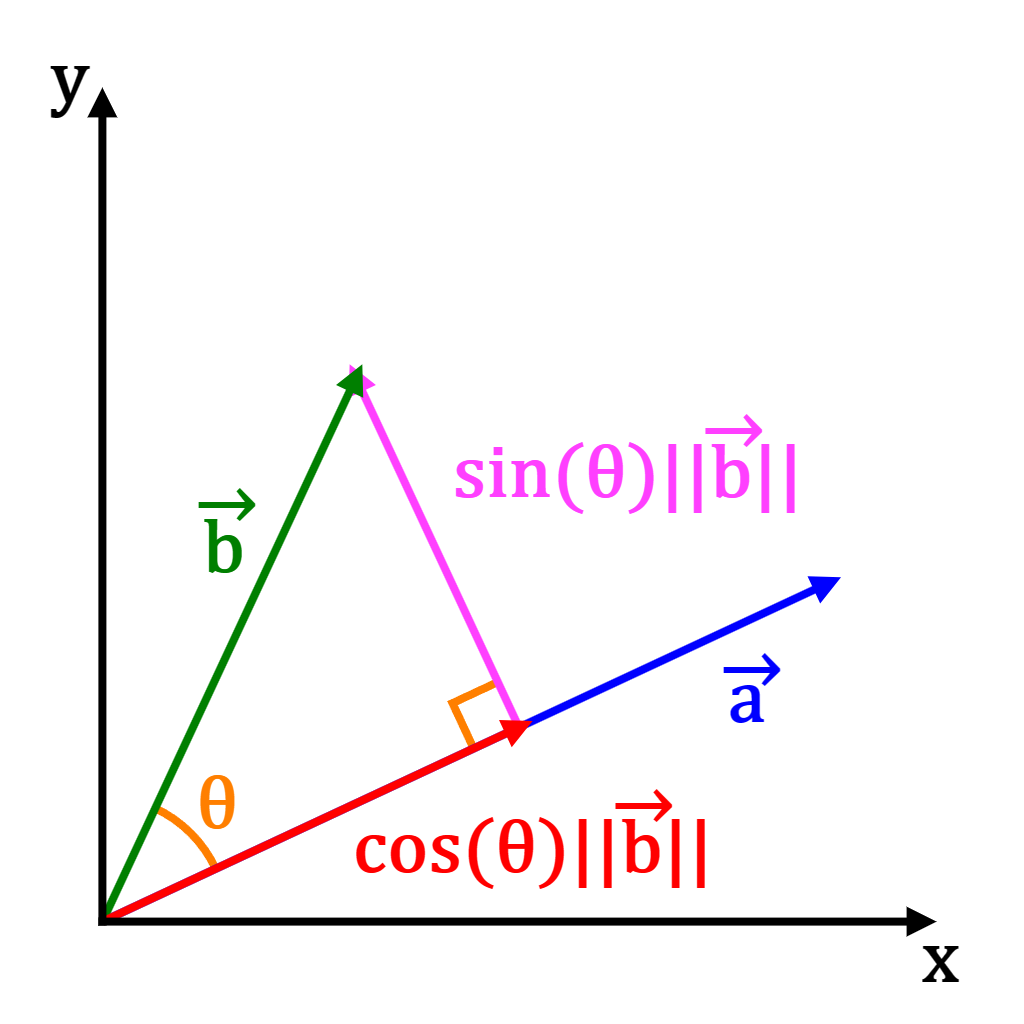
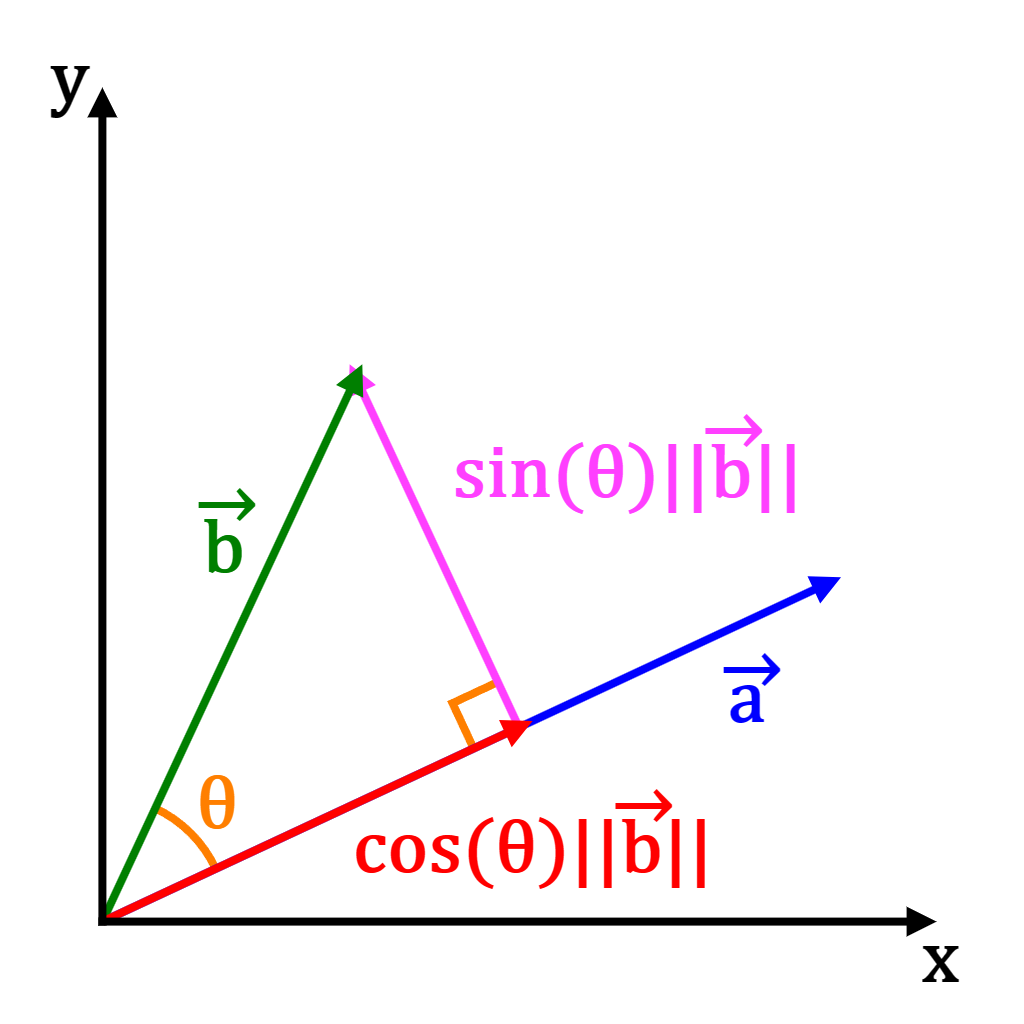
Vector projection is another common and important operation for computer graphics. The vector projection of the vector

\vec{b}

onto the vector

\vec{a}

, denoted by

{proj}_{\vec{a}} \vec{b}

, gives the vector part of

\vec{b}

parallel to

\vec{a}

. The calculation of vector projection is:

{proj}_{\vec{a}} \vec{b} = \cos (θ) \cdot || \vec{b} || \cdot \frac{\vec{a}}{|| \vec{a} ||}

Note: \frac{\vec{a}}{|| \vec{a} ||} is the unit vector in the direction of \vec{a}

Note: \cos (θ) \cdot || \vec{b} || is the length of the projected vector

Note: θ is the angle between \vec{a} and \vec{b}

Recall: \vec{a} \cdot \vec{b} = || \vec{a} || \cdot || \vec{b} || \cdot \cos (θ) \Rightarrow \cos (θ) = \frac{\vec{a} \cdot \vec{b}}{|| \vec{a} || \cdot || \vec{b} ||}

= \frac{\vec{a} \cdot \vec{b}}{|| \vec{a} || \cdot || \vec{b} ||} \cdot || \vec{b} || \cdot \frac{\vec{a}}{|| \vec{a} ||}

= \frac{\vec{a} \cdot \vec{b}}{|| \vec{a} || \cdot || \vec{a} ||} \vec{a}

Recall: || \vec{a} || \cdot || \vec{a} || = \vec{a} \cdot \vec{a}

= \frac{\vec{a} \cdot \vec{b}}{\vec{a} \cdot \vec{a}} \vec{a}

Matrices:

Matrices are arrays of vectors which can be used to apply transformations to vectors.In 3D, we commonly use 2x2, 3x3, and 4x4 matrices for 2D, 3D, and 4D vectors respectively. A matrix has the form:

[\begin{matrix} R_{00} & R_{01} & ... \\ R_{10} & R_{11} & ... \\ ... & ... & ... \end{matrix}]

A matrix can transform a vector by matrix vector multiplication, which is calculated by multiplying each row of the matrix by the vector to form a new vector. Example 3D matrix vector calculation:

[\begin{matrix} M_{00} & M_{01} & M_{02} \\ M_{10} & M_{11} & M_{12} \\ M_{20} & M_{21} & M_{22} \end{matrix}] [\begin{matrix} V_{x} \\ V_{y} \\ V_{z} \end{matrix}]

= [\begin{matrix} M_{00} \cdot V_{x} + M_{01} \cdot V_{y} + M_{02} \cdot V_{z} \\ M_{10} \cdot V_{x} + M_{11} \cdot V_{y} + M_{12} \cdot V_{z} \\ M_{20} \cdot V_{x} + M_{21} \cdot V_{y} + M_{22} \cdot V_{z} \end{matrix}]

Matrices can be combined together using matrix multiplication, which involves using the dot product on the rows of one matrix with the columns of the other matrix:

[\begin{matrix} M_{00} & M_{01} & M_{02} \\ M_{10} & M_{11} & M_{12} \\ M_{20} & M_{21} & M_{22} \end{matrix}] [\begin{matrix} N_{00} & N_{01} & N_{02} \\ N_{10} & N_{11} & N_{12} \\ N_{20} & N_{21} & N_{22} \end{matrix}]

= [\begin{matrix} [M_{00}, M_{01}, M_{02}] \cdot [N_{00}, N_{10}, N_{20}] & [M_{00}, M_{01}, M_{02}] \cdot [N_{01}, N_{11}, N_{21}] & [M_{00}, M_{01}, M_{02}] \cdot [N_{02}, N_{12}, N_{22}] \\ [M_{10}, M_{11}, M_{12}] \cdot [N_{00}, N_{10}, N_{20}] & [M_{10}, M_{11}, M_{12}] \cdot [N_{01}, N_{11}, N_{21}] & [M_{10}, M_{11}, M_{12}] \cdot [N_{02}, N_{12}, N_{22}] \\ [M_{20}, M_{21}, M_{22}] \cdot [N_{00}, N_{10}, N_{20}] & [M_{20}, M_{21}, M_{22}] \cdot [N_{01}, N_{11}, N_{21}] & [M_{20}, M_{21}, M_{22}] \cdot [N_{02}, N_{12}, N_{22}] \end{matrix}]

= [\begin{matrix} (M_{00} \cdot N_{00} + M_{01} \cdot N_{10} + M_{02} \cdot N_{20}) & (M_{00} \cdot N_{01} + M_{01} \cdot N_{11} + M_{02} \cdot N_{21}) & (M_{00} \cdot N_{02} + M_{01} \cdot N_{12} + M_{02} \cdot N_{22}) \\ (M_{10} \cdot N_{00} + M_{11} \cdot N_{10} + M_{12} \cdot N_{20}) & (M_{10} \cdot N_{01} + M_{11} \cdot N_{11} + M_{12} \cdot N_{21}) & (M_{10} \cdot N_{02} + M_{11} \cdot N_{12} + M_{12} \cdot N_{22}) \\ (M_{20} \cdot N_{00} + M_{21} \cdot N_{10} + M_{22} \cdot N_{20}) & (M_{20} \cdot N_{01} + M_{21} \cdot N_{11} + M_{22} \cdot N_{21}) & (M_{20} \cdot N_{02} + M_{21} \cdot N_{12} + M_{22} \cdot N_{22}) \end{matrix}]

Sources:

Wikipedia - Vector (mathematics and physics): https://en.wikipedia.org/wiki/Vector_(mathematics_and_physics)
Wikipedia - Dot product: https://en.wikipedia.org/wiki/Dot_product
Wikipedia - Cross product: https://en.wikipedia.org/wiki/Cross_product
Wikipedia - Vector projection: https://en.wikipedia.org/wiki/Vector_projection