Introduction:

This tutorial explains how quaternions work and how they can be used to produce 3D rotations. Basics of linear algebra and trigonometry are required for this tutorial. Complex numbers and polar coordinates are also important, but the important parts are summarized in the next background section. This tutorial works its way up from 2D rotations and how its related to complex numbers, and then it extends that to the 3D space to show how quaternions produce 3D rotations.

Quaternions are very common in computer graphics and animation because of some useful properties, such as avoiding gimbal lock, which is a major problem with euler angles.

Background:

Polar coordinates:

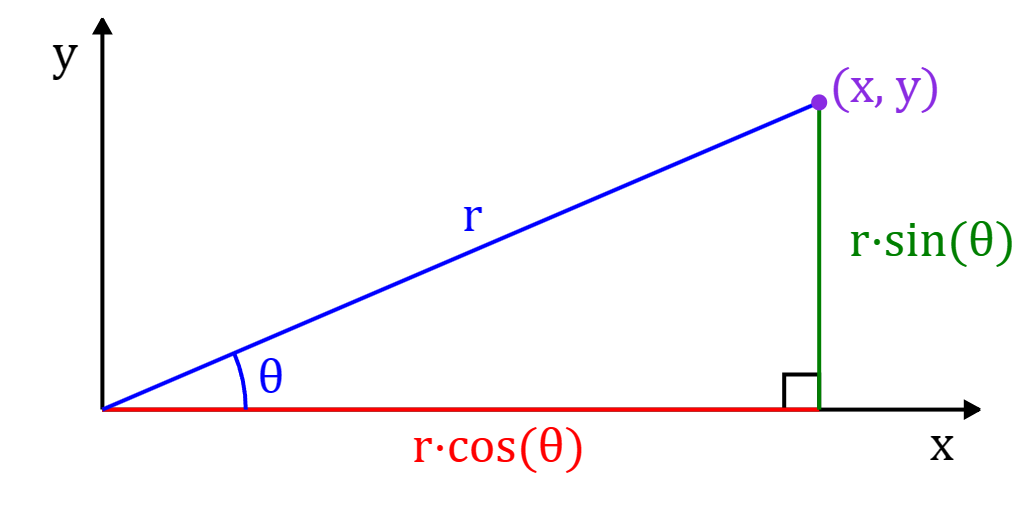
Polar coordinates are coordinates expressed in terms of angle

θ

and magnitude

r

.

A cartesian coordinate

(x, y)

is equivalent to the polar coordinate

(r, θ)

where:

r = \sqrt{x^{2} + y^{2}}

θ = \arctan (y, x)

Polar coordiantes can be converted back into cartesian coordinates using the properties of

\sin

and

\cos

:

\cos (θ) = \frac{x}{r} \Rightarrow x = r \cdot \cos (θ)

\sin (θ) = \frac{y}{r} \Rightarrow y = r \cdot \sin (θ)

Complex numbers:

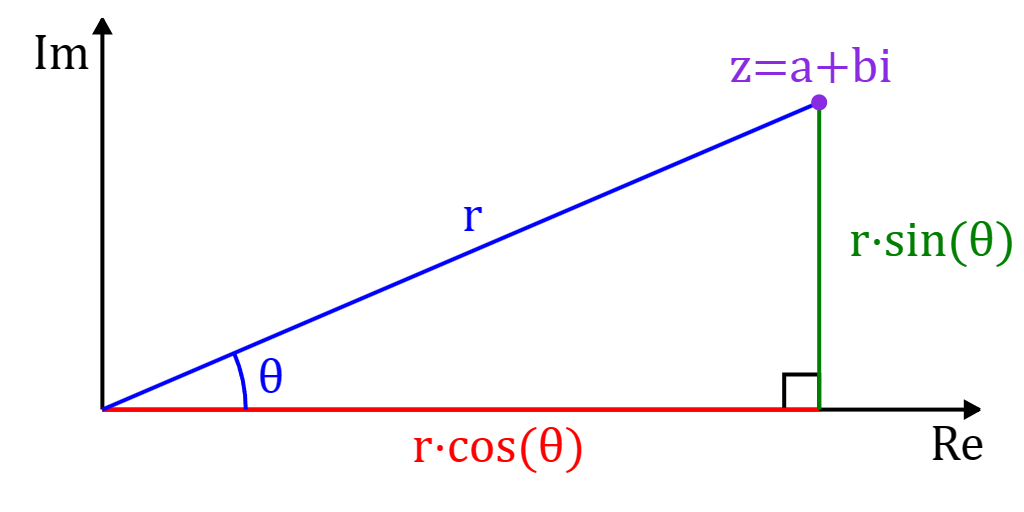
Complex numbers have the form

z = a + b i

, where

a

is the real part,

b

is the imaginary part, and

i

is the imaginary unit which is the square root of

- 1

. In other words,

i^{2} = - 1

.

Complex numbers can be represented in both cartesian and polar coordinates. In cartesian coordinates, the

x

axis is the real axis, and the

y

axis is the imaginary axis:

z = x + y i

Similarly, a complex number

z = a + b i

can be expressed as polar coordinates by substituting:

a = r \cdot \cos (θ)

b = r \cdot \sin (θ)

This gives us:

z = (r \cdot \cos (θ)) + (r \cdot \sin (θ)) \cdot i

= r \cdot (\cos (θ) + \sin (θ) \cdot i)

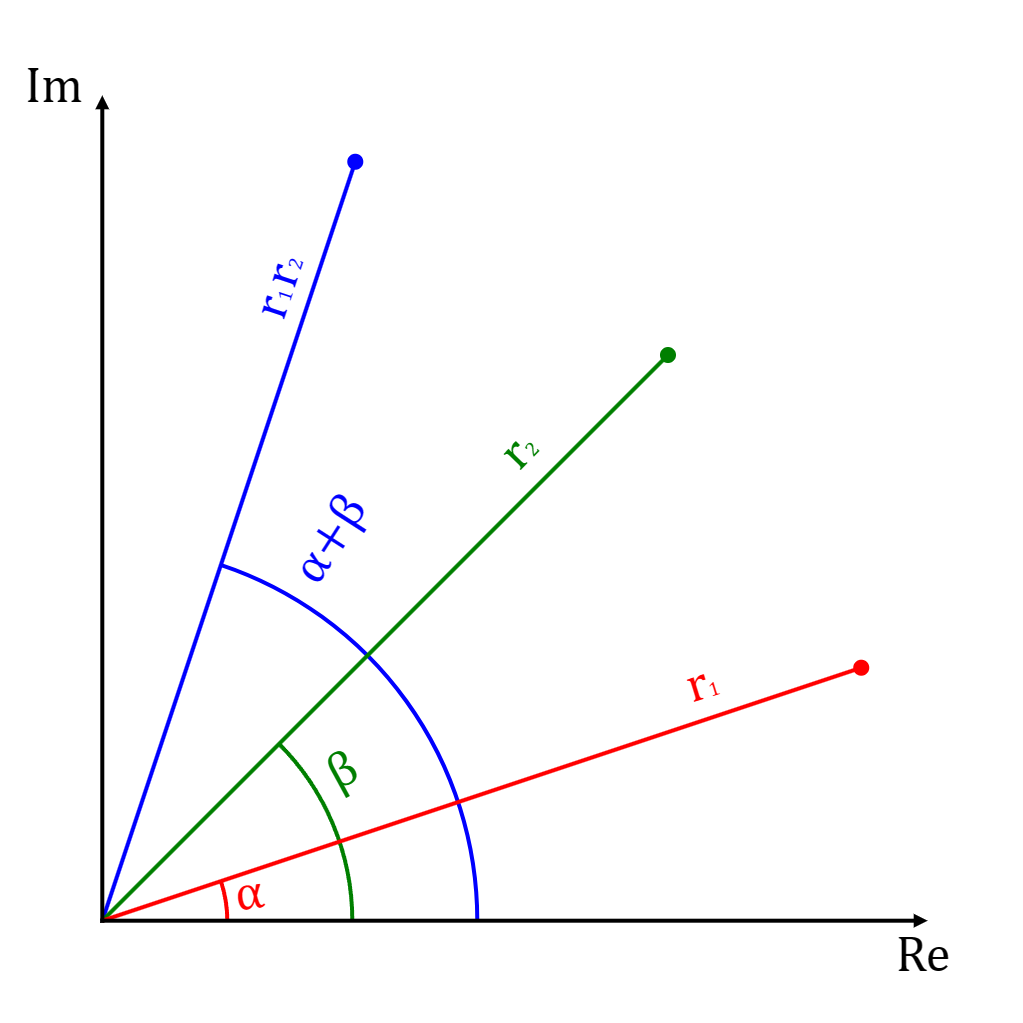
Two complex numbers

z_{1} = a_{1} + b_{1} i

and

z_{2} = a_{2} + b_{2} i

can be multiplied as follows:

z_{1} \cdot z_{2} = (a_{1} + b_{1} i) \cdot (a_{2} + b_{2} i)

= a_{1} a_{2} + a_{1} b_{2} i + a_{2} b_{1} i + b_{1} b_{2} i^{2}

= a_{1} a_{2} + a_{1} b_{2} i + a_{2} b_{1} i - b_{1} b_{2}

= (a_{1} a_{2} - b_{1} b_{2}) + (a_{1} b_{2} + a_{2} b_{1}) i

In polar coordinates, this multiplication is equivalent to:

z_{1} z_{2} = r_{1} (\cos (θ_{1}) + \sin (θ_{1}) i) \cdot r_{2} (\cos (θ_{2}) + \sin (θ_{2}) i)

= r_{1} r_{2} ((\cos (θ_{1}) + \sin (θ_{1}) i) \cdot (\cos (θ_{2}) + \sin (θ_{2}) i))

= r_{1} r_{2} (\cos (θ_{1}) \cos (θ_{2}) + \cos (θ_{1}) \sin (θ_{2}) i + \sin (θ_{1}) \cos (θ_{2}) i + \sin (θ_{1}) \sin (θ_{2}) i^{2})

= r_{1} r_{2} ((\cos (θ_{1}) \cos (θ_{2}) - \sin (θ_{1}) \sin (θ_{2})) + (\cos (θ_{1}) \sin (θ_{2}) + \sin (θ_{1}) \cos (θ_{2})) i)

Then simplying with trigonometric identities, we get:

= r_{1} r_{2} (\cos (θ_{1} + θ_{2}) + \sin (θ_{1} + θ_{2}) i)

In other words, multiplying two complex numbers creates a new complex number where the original angles have added up, and the magnitudes have multiplied.

Complex numbers and 2D rotation:

Let's say you have a cartesian point

(x_{1}, y_{1})

and you want to rotate it by

β

radians.

As shown in the background section, this point

(x_{1}, y_{1})

is equivalent to the polar coordinate

(r, α)

such that:

x_{1} = r \cdot \cos (α)

y_{1} = r \cdot \sin (α)

When this point is rotated by

β

radians, we get a new point

(x_{2}, y_{2})

which is equivalent to the polar coordinate

(r, α + β)

:

x_{2} = r \cdot \cos (α + β)

y_{2} = r \cdot \sin (α + β)

Expanding this out using the trigonometric identities, we get:

x_{2} = r (\cos (α) \cos (β) - \sin (α) \sin (β))

y_{2} = r (\sin (α) \cos (β) + \cos (α) \sin (β))

Note that as shown in the background section of complex number multiplication, this is equivalent to multiplying the complex numbers

(r, α)

and

(1, β)

:

r (\cos (α) + \sin (α) i) \cdot 1 (\cos (β) + \sin (β) i)

= r (\cos (α) \cos (β) - \sin (α) \sin (β)) + r (\cos (α) \sin (β) + \sin (α) \cos (β)) i

= x_{2} + y_{2} i

Simplying using trigonometric identities, this can be simplified to:

r (\cos (α) \cos (β) - \sin (α) \sin (β)) + r (\cos (α) \sin (β) + \sin (α) \cos (β)) i

= r (\cos (α + β) + \sin (α + β) i)

This means complex numbers with magnitude 1 naturally encode 2D rotation; multiplying a point

(x, y)

with a complex number

(1, θ)

rotates the point by

θ

. For example, let's say you want to rotate a point by

\frac{π}{2}

radians, this is equivalent to the complex number:

\cos (\frac{π}{2}) + \sin (\frac{π}{2}) i

= 0 + 1 \cdot i

= i

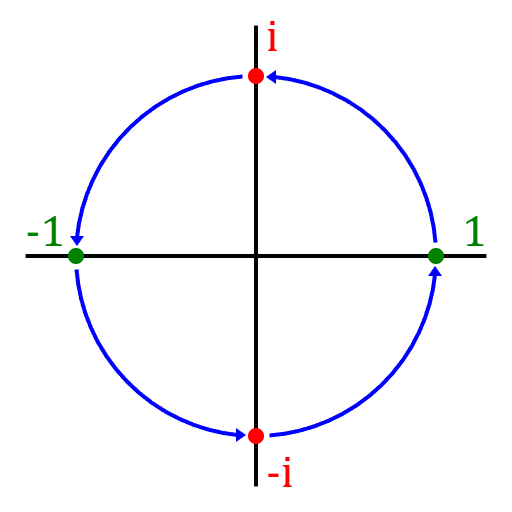
This shows us that multiplying by

i

is equivalent to rotating by

\frac{π}{2}

radians. See this picture which shows multiplication by

i

on the key points

+ 1

,

+ i

,

- 1

, and

- i

:

(+ 1) \cdot i = (+ i)

(+ i) \cdot i = (- 1)

(- 1) \cdot i = (- i)

(- i) \cdot i = (+ 1)

Representing 2D rotations as matrices:

As shown in the previous section, the point

(x_{1}, y_{1}) = (r \cdot \cos (θ_{1}), r \cdot \sin (θ_{1}))

can be rotated by

θ

as follows:

x_{2} = r (\cos (θ_{1}) \cos (θ) - \sin (θ_{1}) \sin (θ))

y_{2} = r (\sin (θ_{1}) \cos (θ) + \cos (θ_{1}) \sin (θ))

This can be expressed as the matrix vector multiplication:

[\begin{matrix} x_{2} \\ y_{2} \end{matrix}] = [\begin{matrix} \cos (θ) & - \sin (θ) \\ \sin (θ) & \cos (θ) \end{matrix}] [\begin{matrix} r \cos (θ_{1}) \\ r \sin (θ_{1}) \end{matrix}]

= [\begin{matrix} \cos (θ) & - \sin (θ) \\ \sin (θ) & \cos (θ) \end{matrix}] [\begin{matrix} x_{1} \\ y_{1} \end{matrix}]

Another way to derive this matrix is represent

1

and

i

as matrices:

1 = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] i = [\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}]

This means the rotation complex number

\cos (θ) + \sin (θ) i

can be expressed as:

\cos (θ) [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] + \sin (θ) [\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}]

= [\begin{matrix} \cos (θ) & - \sin (θ) \\ \sin (θ) & \cos (θ) \end{matrix}]

Euler's formula:

Euler's formula states that

e^{i x} = \cos (x) + i \cdot \sin (x)

. This can be shown as follows:

The Maclaurin expansion of

\sin (x)

is:

\sin (x) = \frac{x^{1}}{1!} - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + \frac{x^{9}}{9!} - ...

The Maclaurin expansion of

\cos (x)

is:

\cos (x) = \frac{x^{0}}{0!} - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + \frac{x^{8}}{8!} - ...

The Maclaurin expansion of

e^{x}

is:

e^{x} = \frac{x^{0}}{0!} + \frac{x^{1}}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \frac{x^{4}}{4!} + ...

This means that putting

e

to the power of

i x

gives:

e^{i x} = \frac{{(i x)}^{0}}{0!} + \frac{{(i x)}^{1}}{1!} + \frac{{(i x)}^{2}}{2!} + \frac{{(i x)}^{3}}{3!} + \frac{{(i x)}^{4}}{4!} + \frac{{(i x)}^{5}}{5!} + \frac{{(i x)}^{6}}{6!} + \frac{{(i x)}^{7}}{7!} + \frac{{(i x)}^{8}}{8!} + \frac{{(i x)}^{9}}{9!} ...

= \frac{x^{0}}{0!} + \frac{x^{1}}{1!} i - \frac{x^{2}}{2!} - \frac{x^{3}}{3!} i + \frac{x^{4}}{4!} + \frac{x^{5}}{5!} i - \frac{x^{6}}{6!} - \frac{x^{7}}{7!} i + \frac{x^{8}}{8!} + \frac{x^{9}}{9!} i - ...

= (\frac{x^{0}}{0!} - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + \frac{x^{8}}{8!} - ...) + i \cdot (\frac{x^{1}}{1!} - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + \frac{x^{9}}{9!} - ...)

= \cos (x) + i \cdot \sin (x)

Using Euler's formula, a rotation of the vector

\vec{v} = (x, y)

by

θ

, can be expressed as follows:

e^{i θ} \cdot \vec{v} = (\cos (θ) + i \cdot \sin (θ)) \cdot (x + i \cdot y)

3D Rotation:

TODO: INSERT LIVE LINK

A vector

\vec{v}

can be rotated in 3D space around any given unit vector

\vec{u}

representing the axis of rotation using Rodrigues' rotation formula:

{\vec{v}}_{rot} = \cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v}) + (1 - \cos (θ)) (\vec{u} \cdot \vec{v}) \vec{u}

Note that

{\vec{v}}_{rot}

is

\vec{v}

rotated

θ

radians around

\vec{u}

.

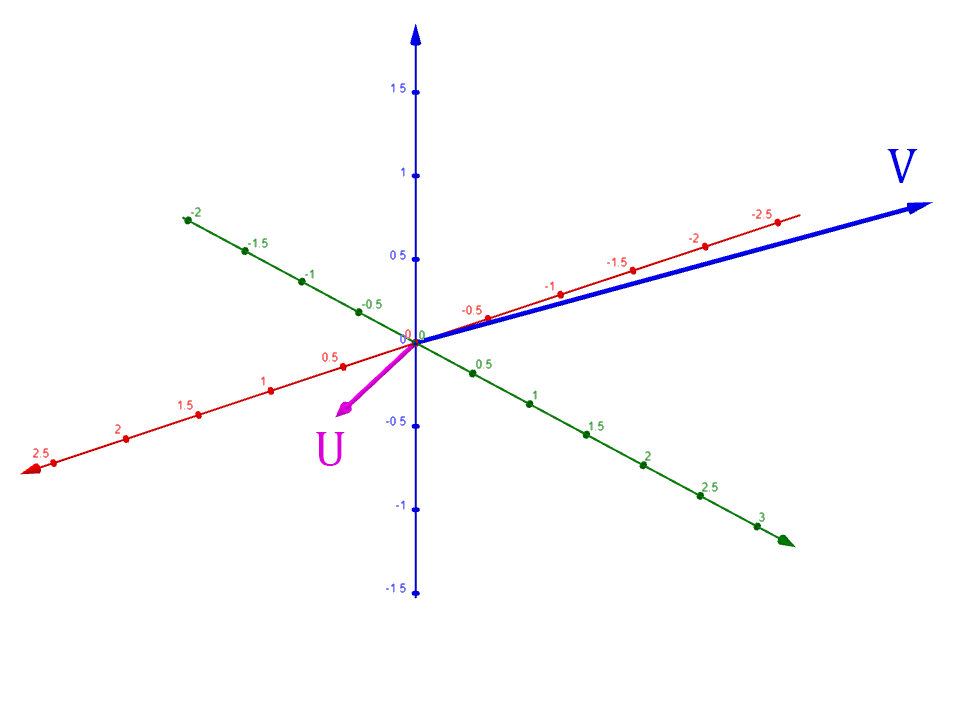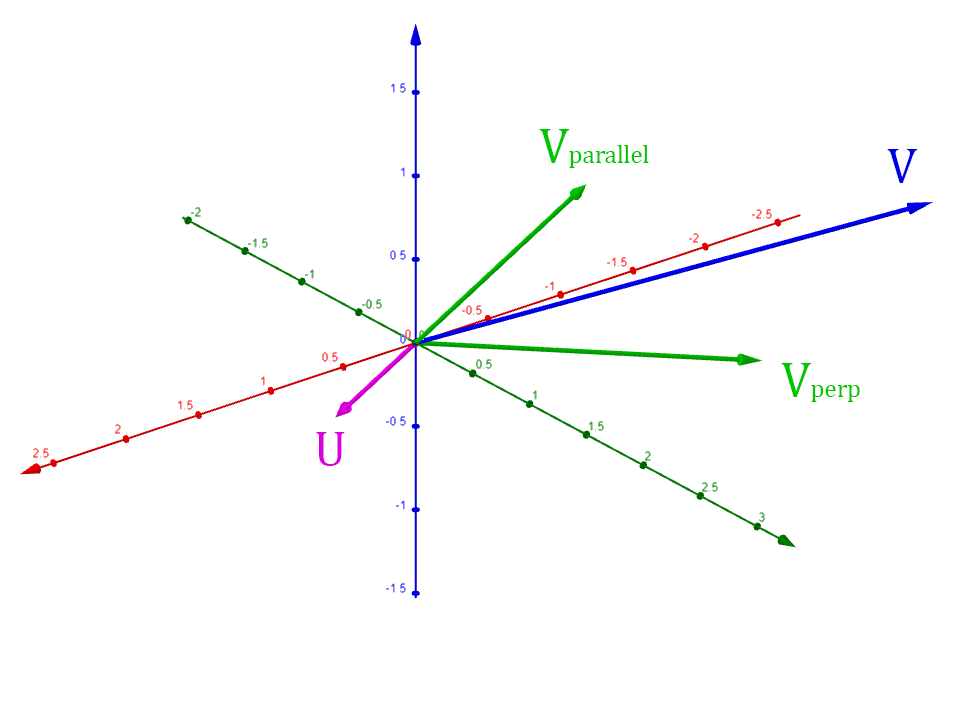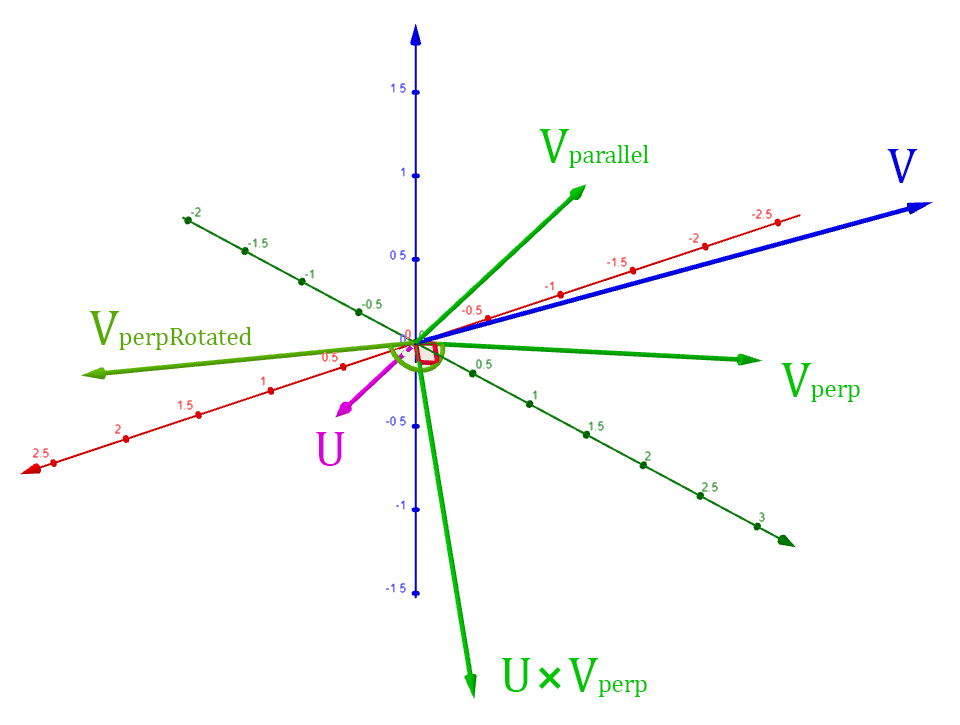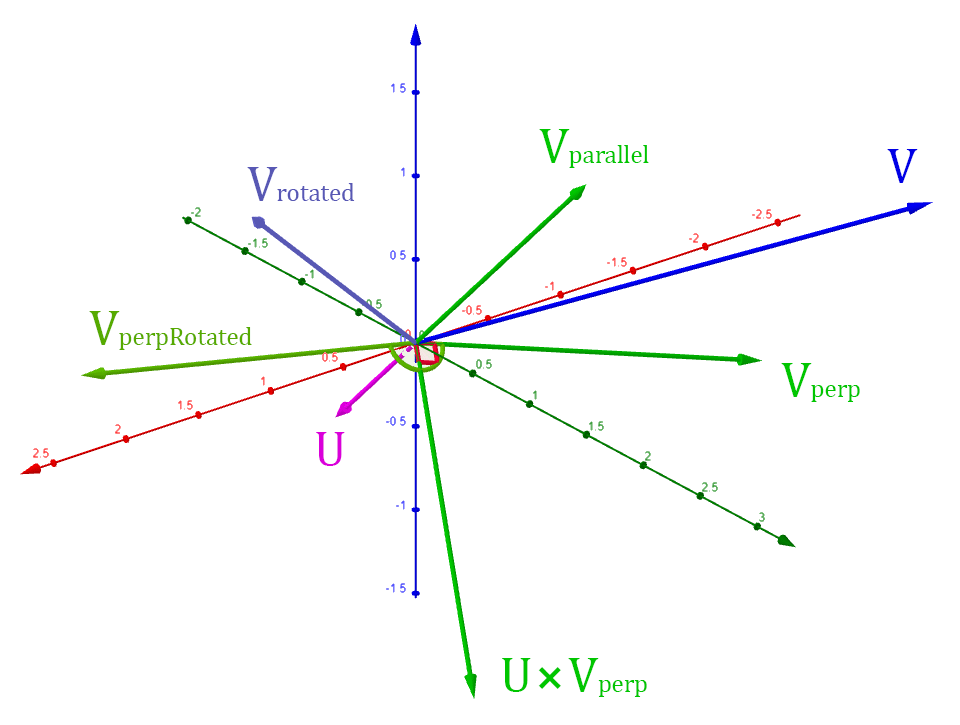
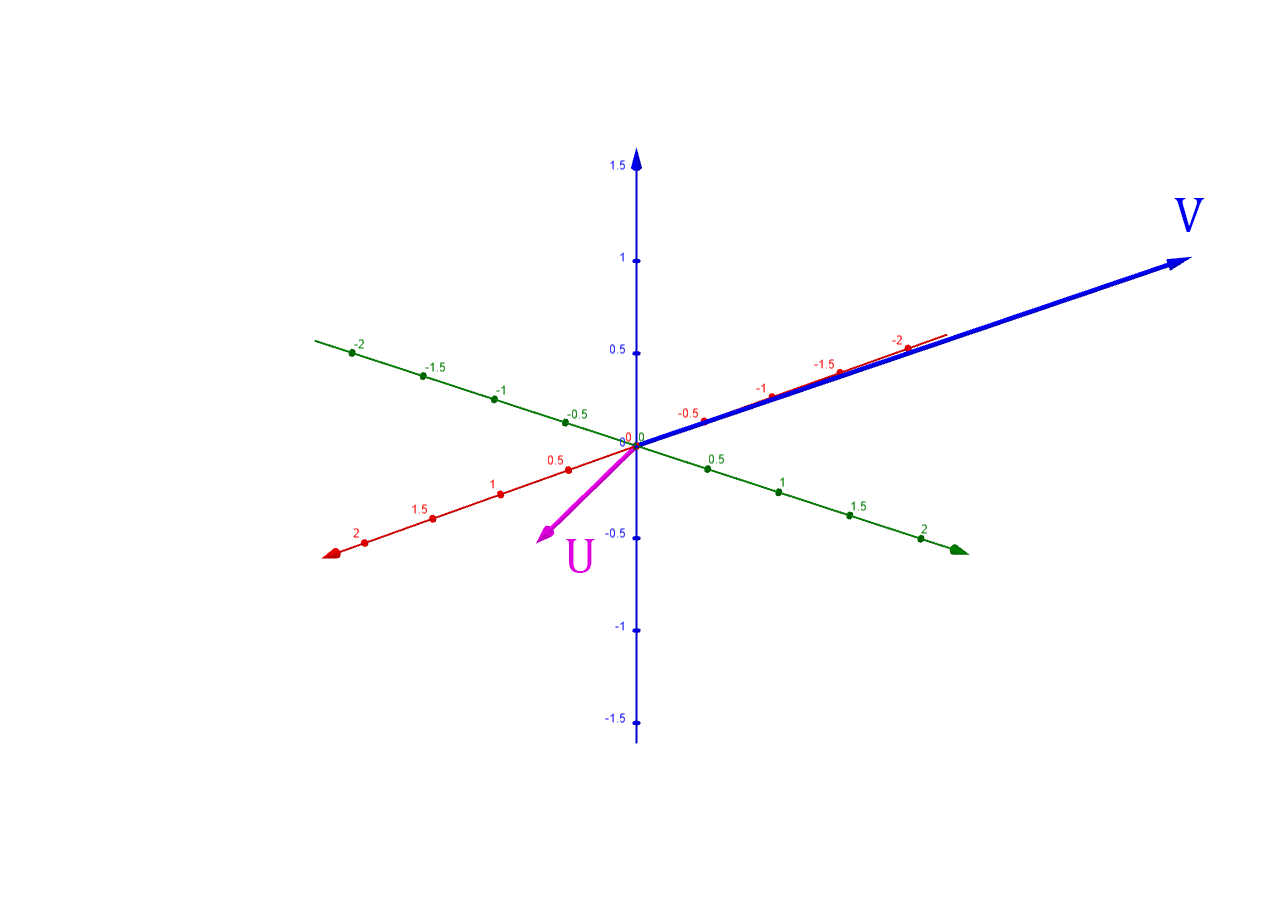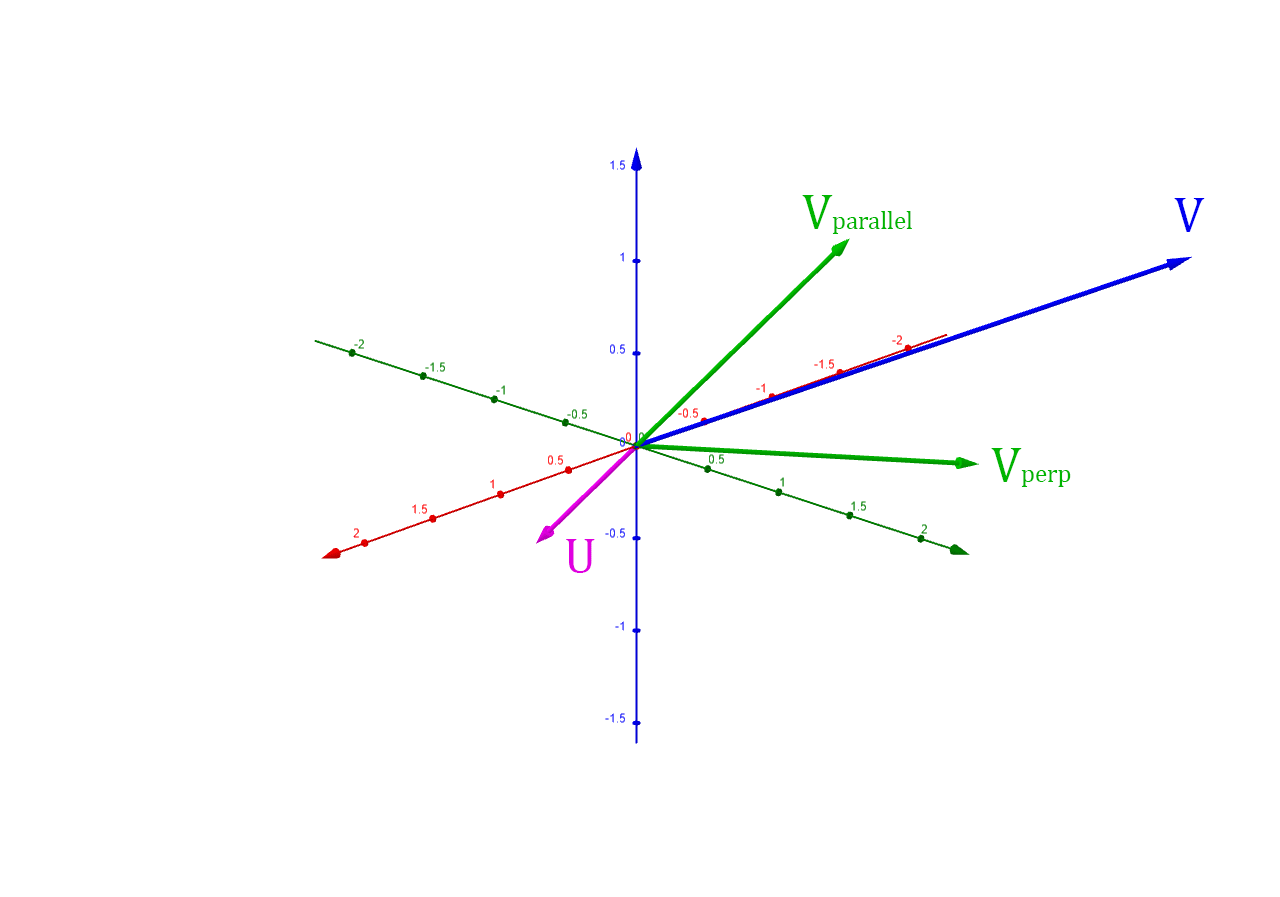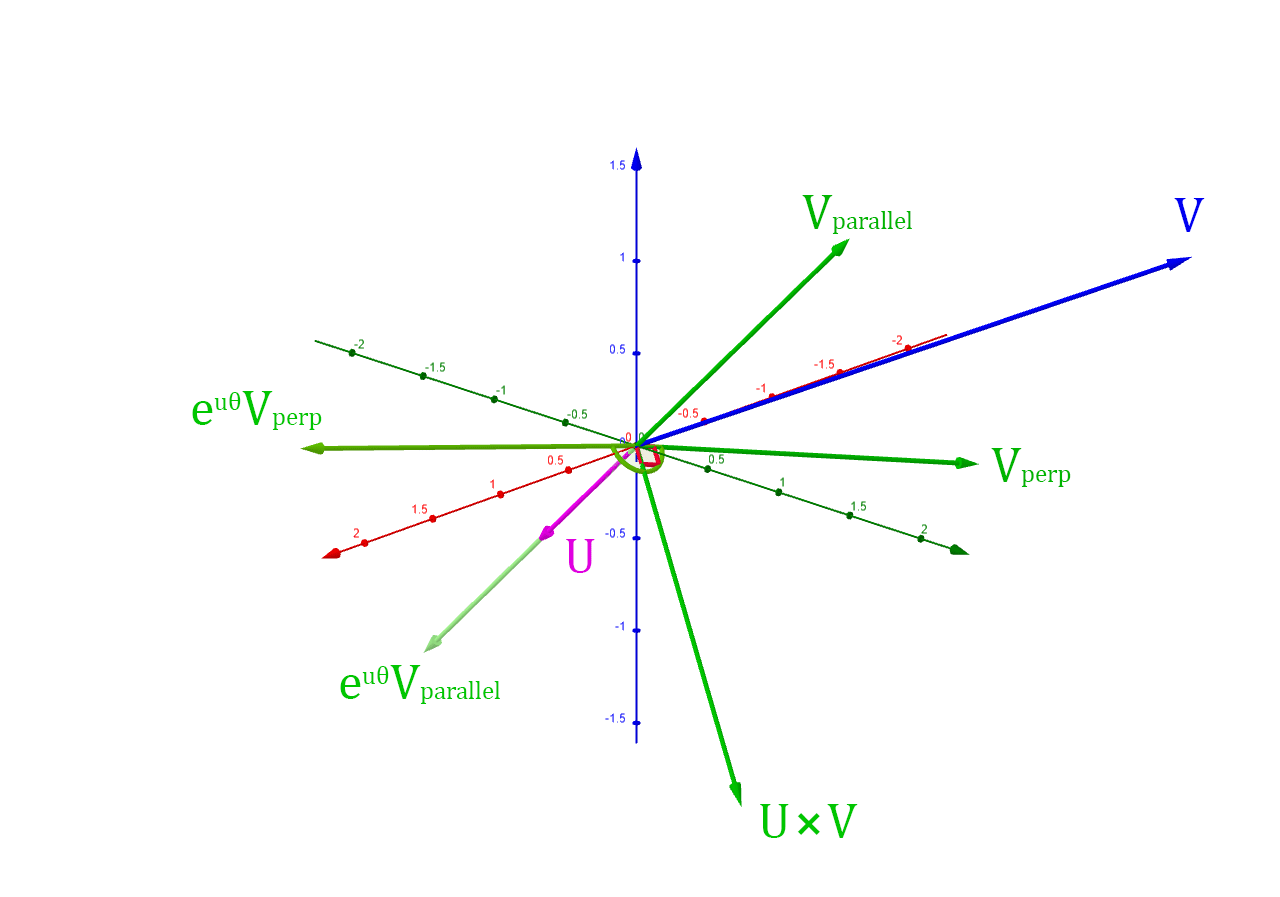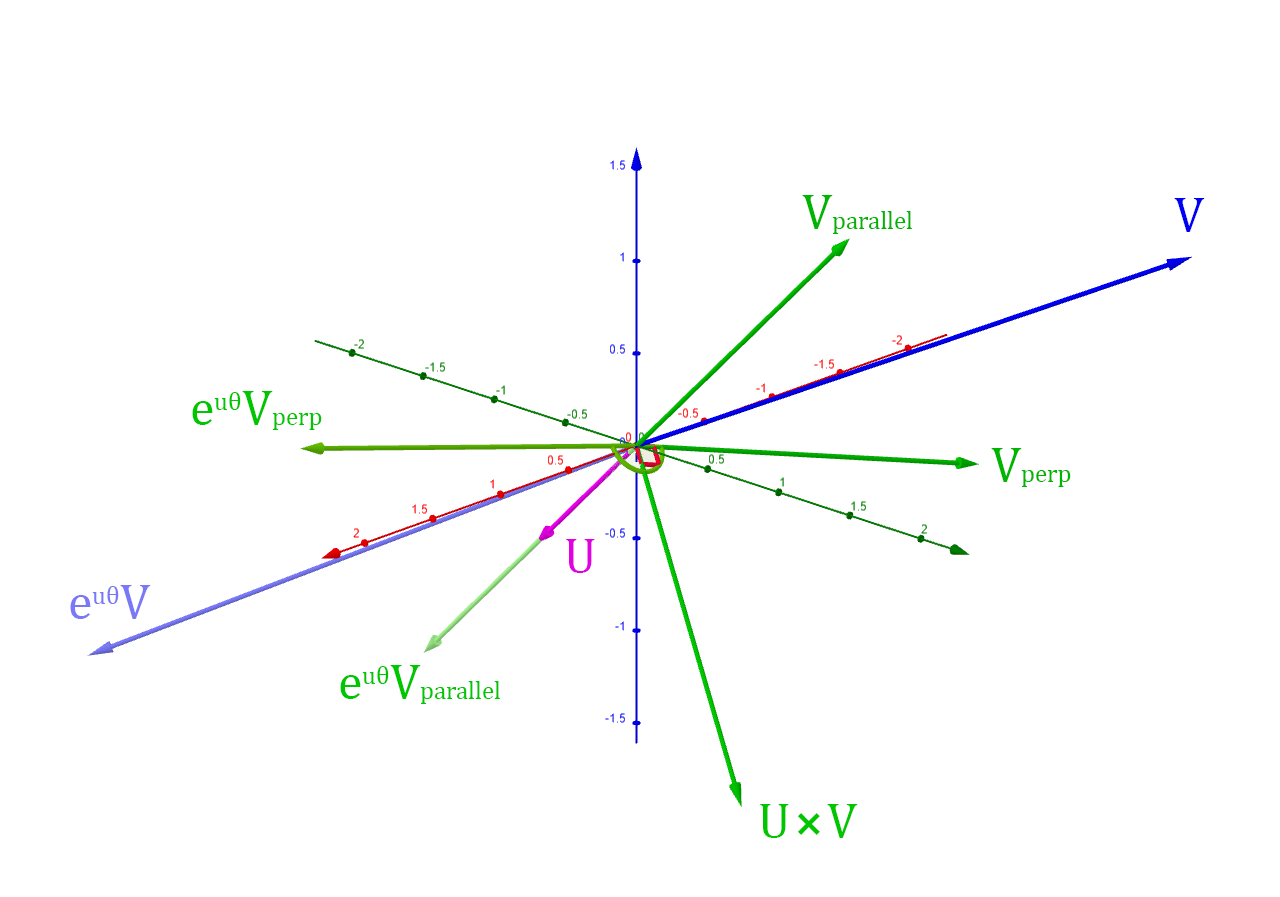
To derive this formula, we start by breaking the vector

\vec{v}

into

{\vec{v}}_{∥}

and

{\vec{v}}_{⊥}

such that:

${\vec{v}}_{∥} + {\vec{v}}_{⊥} = \vec{v}$
${\overset{v}{=}}_{∥}$ is the part of $\vec{v}$ parallel to $\vec{u}$
${\vec{v}}_{⊥}$ is the part of $\vec{v}$ perpendicular to $\vec{u}$

The parallel vector

{\vec{v}}_{∥}

is the projection of

\vec{v}

onto

\vec{u}

:

{\vec{v}}_{∥} = \frac{\vec{v} \cdot \vec{u}}{\vec{u} \cdot \vec{u}} \vec{u}

= \frac{\vec{v} \cdot \vec{u}}{{|| \vec{u} ||}^{2}} \vec{u}

Note that

{|| \vec{u} ||}^{2} = 1

since

\vec{u}

is a unit vector, so we have:

{\vec{v}}_{∥} = (\vec{v} \cdot \vec{u}) \vec{u}

After

{\vec{v}}_{∥}

is found, we can calulate

{\vec{v}}_{⊥}

as follows:

{\vec{v}}_{⊥} = \vec{v} - {\vec{v}}_{∥}

= \vec{v} - (\vec{v} \cdot \vec{u}) \vec{u}

When the rotation

θ

is applied,

{\vec{v}}_{∥}

will remain the same, and

{\vec{v}}_{⊥}

will rotate on the plane with the normal

\vec{u}

. This means the rotated vector

{\vec{v}}_{rot}

will be a sum of

{\vec{v}}_{∥}

and

{\vec{v}}_{⊥rot}

:

{\vec{v}}_{rot} = {\vec{v}}_{∥} + {\vec{v}}_{⊥rot} .

Note that

{\vec{v}}_{⊥rot}

is

{\vec{v}}_{⊥}

rotated

θ

radians on the plane with normal

\vec{u}

.

The vector

\vec{u} \times {\vec{v}}_{⊥}

is

{\vec{v}}_{⊥}

rotated

\frac{π}{2}

radians on the plane with the normal

\vec{u}

. The rotated perpendicular vector

{\vec{v}}_{⊥rot}

will be a sum of this vector

\vec{u} \times {\vec{v}}_{⊥}

and

{\vec{v}}_{⊥}

:

These vectors can be used to calculate the rotated perpendicular vector

{\vec{v}}_{⊥rot}

using sine and cosine:

{\vec{v}}_{⊥rot} = \cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})

All of these definitions can be combined to form the rotation formula:

{\vec{v}}_{rot} = {\vec{v}}_{∥} + {\vec{v}}_{⊥rot}

= {\vec{v}}_{∥} + \cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})

= {\vec{v}}_{∥} + \cos (θ) (\vec{v} - {\vec{v}}_{∥}) + \sin (θ) (\vec{u} \times (\vec{v} - {\vec{v}}_{∥}))

= {\vec{v}}_{∥} + \cos (θ) \vec{v} - \cos (θ) {\vec{v}}_{∥} + \sin (θ) (\vec{u} \times \vec{v} - \vec{u} \times {\vec{v}}_{∥})

Note: \vec{u} \times {\vec{v}}_{∥} = 0 since \vec{u} and {\vec{v}}_{∥} are parallel

= \cos (θ) \vec{v} + {\vec{v}}_{∥} - \cos (θ) {\vec{v}}_{∥} + \sin (θ) (\vec{u} \times \vec{v})

= \cos (θ) \vec{v} + (1 - \cos (θ)) {\vec{v}}_{∥} + \sin (θ) (\vec{u} \times \vec{v})

{\vec{v}}_{rot} = \cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v}) + (1 - \cos (θ)) (\vec{u} \cdot \vec{v}) \vec{u}

This formula can be converted into a matrix multiplication by factoring out the original vector

\vec{v}

:

\cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v}) + (1 - \cos (θ)) (\vec{u} \cdot \vec{v}) \vec{u}

\cos (θ) (v_{x} i + v_{y} j + v_{z} k) + \sin (θ) | \begin{matrix} i & j & k \\ u_{x} & u_{y} & u_{z} \\ v_{x} & v_{y} & v_{z} \end{matrix} | + (1 - \cos (θ)) (u_{x} v_{x} + u_{y} v_{y} + u_{z} v_{z}) (u_{x} i + u_{y} j + u_{z} k)

= \cos (θ) (v_{x} i + v_{y} j + v_{z} k) + \sin (θ) ((u_{y} v_{z} - u_{z} v_{y}) i - (u_{x} v_{z} - u_{z} v_{x}) j + (u_{x} v_{y} - u_{y} v_{x}) k) + (1 - \cos (θ)) (u_{x} v_{x} + u_{y} v_{y} + u_{z} v_{z}) (u_{x} i + u_{y} j + u_{z} k)

= (\cos (θ) v_{x} + \sin (θ) (u_{y} v_{z} - u_{z} v_{y}) + (1 - \cos (θ)) (u_{x} v_{x} + u_{y} v_{y} + u_{z} v_{z}) u_{x}) i

+ (\cos (θ) v_{y} - \sin (θ) (u_{x} v_{z} - u_{z} v_{x}) + (1 - \cos (θ)) (u_{x} v_{x} + u_{y} v_{y} + u_{z} v_{z}) u_{y}) j

+ (\cos (θ) v_{z} + \sin (θ) (u_{x} v_{y} - u_{y} v_{x}) + (1 - \cos (θ)) (u_{x} v_{x} + u_{y} v_{y} + u_{z} v_{z}) u_{z}) k

= [\begin{matrix} \cos (θ) + (1 - \cos (θ)) {u_{x}}^{2} & - \sin (θ) u_{z} + (1 - \cos (θ)) u_{x} u_{y} & \sin (θ) u_{y} + (1 - \cos (θ)) u_{x} u_{z} \\ \sin (θ) u_{z} + (1 - \cos (θ)) u_{x} u_{y} & \cos (θ) + (1 - \cos (θ)) {u_{y}}^{2} & - \sin (θ) u_{x} + (1 - \cos (θ)) u_{y} u_{z} \\ - \sin (θ) u_{y} + (1 - \cos (θ)) u_{x} u_{z} & \sin (θ) u_{x} + (1 - \cos (θ)) u_{y} u_{z} & \cos (θ) + (1 - \cos (θ)) {u_{z}}^{2} \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}]

= R_{(u_{x}, u_{y}, u_{z}), θ} \vec{v}

To use Euler angles, this matrix can be turned into seperate matrices for each axis

x

,

y

, and

z

:

R_{x} = R_{(1, 0, 0), θ} = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos (θ) & - \sin (θ) \\ 0 & \sin (θ) & \cos (θ) \end{matrix}]

R_{y} = R_{(0, 1, 0), θ} = [\begin{matrix} \cos (θ) & 0 & \sin (θ) \\ 0 & 1 & 0 \\ - \sin (θ) & 0 & \cos (θ) \end{matrix}]

R_{z} = R_{(0, 0, 1), θ} = [\begin{matrix} \cos (θ) & - \sin (θ) & 0 \\ \sin (θ) & \cos (θ) & 0 \\ 0 & 0 & 1 \end{matrix}]

Quaternions:

Quaternions are a 4D number system of the form

a + b i + c j + d k

. Quaternions extend the complex number system with 2 additional dimensions

j

and

k

.

This chart (from Wikipedia) shows the multiplication rules for the basis vectors

i

,

j

, and

k

(the left column is the first term and the top column is the second term):

	$1$	$i$	$j$	$k$
$1$	$1$	$i$	$j$	$k$
$i$	$i$	$- 1$	$k$	$- j$
$j$	$j$	$- k$	$- 1$	$i$
$k$	$k$	$j$	$- i$	$- 1$

Note: Row

\times

Column

Note that since the multiplication of the basis vectors is not commutative (i.e.

i \cdot j \neq j \cdot i

), quaternion multiplication is not commutative.

The multiplication result of two quaternions

q_{1}

and

q_{2}

can be derived using this chart:

q_{1} \cdot q_{2} = (a_{1} + b_{1} i + c_{1} j + d_{1} k) \cdot (a_{2} + b_{2} i + c_{2} j + d_{2} k)

= a_{1} a_{2} + a_{1} b_{2} i + a_{1} c_{2} j + a_{1} d_{2} k

+ b_{1} a_{2} i + b_{1} b_{2} i^{2} + b_{1} c_{2} i j + b_{1} d_{2} i k

+ c_{1} a_{2} j + c_{1} b_{2} j i + c_{1} c_{2} j^{2} + c_{1} d_{2} j k

+ d_{1} a_{2} k + d_{1} b_{2} k i + d_{1} c_{2} k j + d_{1} d_{2} k^{2}

= a_{1} a_{2} + a_{1} b_{2} i + a_{1} c_{2} j + a_{1} d_{2} k

+ b_{1} a_{2} i - b_{1} b_{2} + b_{1} c_{2} k - b_{1} d_{2} j

+ c_{1} a_{2} j - c_{1} b_{2} k - c_{1} c_{2} + c_{1} d_{2} i

+ d_{1} a_{2} k + d_{1} b_{2} j - d_{1} c_{2} i - d_{1} d_{2}

= (a_{1} a_{2} - b_{1} b_{2} - c_{1} c_{2} - d_{1} d_{2})

+ (a_{1} b_{2} + b_{1} a_{2} + c_{1} d_{2} - d_{1} c_{2}) i

+ (a_{1} c_{2} - b_{1} d_{2} + c_{1} a_{2} + d_{1} b_{2}) j

+ (a_{1} d_{2} + b_{1} c_{2} - c_{1} b_{2} + d_{1} a_{2}) k

Quaternions can also be expressed as a pair with a real part

r = a

, and a scalar part

\vec{v} = (b, c, d)

:

q = (r, \vec{v})

In this form, the multiplication can be expressed in terms of dot products and cross products:

q_{1} \cdot q_{2} = (r_{1}, \vec{v_{1}}) \cdot (r_{2}, \vec{v_{2}})

= (r_{1} r_{2} - \vec{v_{1}} \cdot \vec{v_{2}}, r_{1} \vec{v_{2}} + r_{2} \vec{v_{1}} + \vec{v_{1}} \times \vec{v_{2}})

Note that this scalar/vector product is the exact same calculation as the manual multiplication of quaternions derived above:

r_{1} r_{2} - \vec{v_{1}} \cdot \vec{v_{2}} = a_{1} a_{2} - b_{1} b_{2} - c_{1} c_{2} - d_{1} d_{2}

r_{1} \vec{v_{2}} + r_{2} \vec{v_{1}} + \vec{v_{1}} \times \vec{v_{2}} = (a_{1} b_{2} + b_{1} a_{2} + c_{1} d_{2} - d_{1} c_{2}) i + (a_{1} c_{2} - b_{1} d_{2} + c_{1} a_{2} + d_{1} b_{2}) j + (a_{1} d_{2} + b_{1} c_{2} - c_{1} b_{2} + d_{1} a_{2}) k

Lastly, the conjugate of a quaternion

q = (r, \vec{v})

, denoted by

q^{*}

, is simply its vector part multipled by

- 1

:

q^{*} = (r, - \vec{v})

The product of a quaternion

q

and its conjugate

q^{*}

is:

q q^{*} = (r, \vec{v}) (r, - \vec{v})

= (r^{2} + \vec{v} \cdot \vec{v}, r \cdot \vec{v} - r \cdot \vec{v} + (- \vec{v} \times \vec{v}))

= (r^{2} + \vec{v} \cdot \vec{v}, 0)

= a^{2} + b^{2} + c^{2} + d^{2}

This means that if

q

is a unit quaternion, this product

q q^{*}

will be equal to 1. This fact will be useful later on.

Quaternion rotation demo:

Blender animation/demo download

Visualizing how quaternion multiplication represents rotations is extremely helpful for understanding how quaternions can be used to represent 3D rotation.

It is a bit hard to see, but this demo has 3 cubes in it: a center cube, an inner cube, and the outer cube. The center cube represents the real dimension's point

+ 1

. The outer cube's parts all represent the real dimension's point

- 1

.

The colored spheres represent the initial points:

- 1

,

+ 1

,

+ i

,

- i

,

+ j

,

- j

,

+ k

,

- k

.

The inner cube represents the 3D imaginary space of the

i

,

j

, and

k

axis. The colored spheres can identify which dimension an inner part represents (for example: the inner cube part with the red sphere is the

i

dimension).

Lastly, the colored arrows represent a quaternion multiplication. The red arrows represent a multiplication by

+ i

, the green arrows represent a multiplication by

+ j

, and the blue arrows represent a multiplication by

+ k

.

Notice which location each initial point takes after a multiplication. For example, a muliplication by

+ i

causes the initial points to move as follows:

+ i \to - 1

- 1 \to - i

- i \to + 1

+ 1 \to + i

+ j \to - k

- k \to - j

- j \to + k

+ k \to + j

Note that this creates two rotations. The first rotation happens on the

i

axis and follows the regular 2D complex number rules/rotation, and affects the

i

and real dimensions. The second rotation happens on the

j

and

k

axis/dimensions.

This demo shows that quaterion multiplication does a 3D rotation as expected, but also does a 2D rotation which we want to avoid. In the section "Quaternions and 3D rotation", we will discuss this more and show how the additional 2D rotation can be cancelled out to produce just the 3D rotation.

Euler's formula for quaternions:

Euler's formula can be extended to quaternions by expanding the Maclaurin series of

e^{\vec{v} θ}

, where

\vec{v}

is a pure vector quaternion (no scalar part):

e^{\vec{v} θ} = \frac{{(\vec{v} θ)}^{0}}{0!} + \frac{{(\vec{v} θ)}^{1}}{1!} + \frac{{(\vec{v} θ)}^{2}}{2!} + \frac{{(\vec{v} θ)}^{3}}{3!} + \frac{{(\vec{v} θ)}^{4}}{4!} + \frac{{(\vec{v} θ)}^{5}}{5!} + \frac{{(\vec{v} θ)}^{6}}{6!} + \frac{{(\vec{v} θ)}^{7}}{7!} + \frac{{(\vec{v} θ)}^{8}}{8!} + \frac{{(\vec{v} θ)}^{9}}{9!} + ...

Evaluating the first few quaternion terms, we see the pattern:

{(0, \vec{v} θ)}^{0} = ({|| \vec{v} θ ||}^{0}, 0)

{(0, \vec{v} θ)}^{1} = (0, {|| \vec{v} θ ||}^{0} \cdot \vec{v} θ)

{(0, \vec{v} θ)}^{2} = (0, \vec{v} θ) \cdot (0, \vec{v} θ) = (- {|| \vec{v} θ ||}^{2}, \vec{0})

{(0, \vec{v} θ)}^{3} = (- {|| \vec{v} θ ||}^{2}, \vec{0}) \cdot (0, \vec{v} θ) = (0, - {|| \vec{v} θ ||}^{2} \cdot \vec{v} θ)

{(0, \vec{v} θ)}^{4} = (0, - {|| \vec{v} θ ||}^{2} \cdot \vec{v} θ) \cdot (0, \vec{v} θ) = ({|| \vec{v} θ ||}^{4}, \vec{0})

This means

e^{\vec{v} θ}

equals:

e^{\vec{v} θ} = \frac{{|| \vec{v} θ ||}^{0}}{0!} + \frac{{|| \vec{v} θ ||}^{0} \cdot \vec{v} θ}{1!} - \frac{{|| \vec{v} θ ||}^{2}}{2!} - \frac{{|| \vec{v} θ ||}^{2} \cdot \vec{v} θ}{3!} + \frac{{|| \vec{v} θ ||}^{4}}{4!} + \frac{{|| \vec{v} θ ||}^{4} \cdot \vec{v} θ}{5!} - \frac{{|| \vec{v} θ ||}^{6}}{6!} - \frac{{|| \vec{v} θ ||}^{6} \cdot \vec{v} θ}{7!} + \frac{{|| \vec{v} θ ||}^{8}}{8!} + \frac{{|| \vec{v} θ ||}^{8} \cdot \vec{v} θ}{9!} - ...

= (\frac{{|| \vec{v} θ ||}^{0}}{0!} - \frac{{|| \vec{v} θ ||}^{2}}{2!} + \frac{{|| \vec{v} θ ||}^{4}}{4!} - \frac{{|| \vec{v} θ ||}^{6}}{6!} + \frac{{|| \vec{v} θ ||}^{8}}{8!} - ...) + \frac{\vec{v} θ}{|| \vec{v} θ ||} \cdot (\frac{{|| \vec{v} θ ||}^{1}}{1!} - \frac{{|| \vec{v} θ ||}^{3}}{3!} + \frac{{|| \vec{v} θ ||}^{5}}{5!} - \frac{{|| \vec{v} θ ||}^{7}}{7!} + \frac{{|| \vec{v} θ ||}^{9}}{9!} - ...)

= \cos (|| \vec{v} θ ||) + \frac{\vec{v} θ}{|| \vec{v} θ ||} \cdot \sin (|| \vec{v} θ ||)

If

\vec{v}

is a unit vector, we get:

|| \vec{v} || = 1 \Rightarrow || \vec{v} θ || = || \vec{v} || \cdot || θ || = || θ ||

This gives us:

e^{\vec{v} θ} = \cos (|| θ ||) + \frac{\vec{v} θ}{|| θ ||} \cdot \sin (|| θ ||)

This can be simplified further using the following facts:

\cos (θ) = \cos (- θ) for all θ \Rightarrow \cos (|| θ ||) = \cos (θ)

\frac{θ}{|| θ ||} \cdot \sin (|| θ ||) = sign (θ) \sin (|| θ ||) = \sin (θ) for all θ \Rightarrow \frac{\vec{v} θ}{|| θ ||} \cdot \sin (|| θ ||) = \vec{v} \cdot \sin (θ)

This leaves us with:

e^{\vec{v} θ} = \cos (θ) + \vec{v} \cdot \sin (θ)

Quaternions and 3D rotation:

TODO: INSERT LIVE LINK

Applying the quaternion

e^{\vec{u} θ}

to a vector

\vec{v}

produces the result:

e^{\vec{u} θ} \cdot \vec{v}

= (\cos (θ), \sin (θ) \vec{u}) (0, \vec{v})

= (- \sin (θ) (\vec{u} \cdot \vec{v}), \cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v}))

This product is not a pure 3D rotation - it introduces the scalar component

- \sin (θ) (\vec{u} \cdot \vec{v})

, which makes the product a 4D point. Another problem is that the vector parts rotation happens on the plane formed by the vectors

\vec{v}

and

\vec{u} \times \vec{v}

- which is the plane with normal

\vec{v} \times (\vec{u} \times \vec{v})

. Also note that when the angle between

\vec{u}

and

\vec{v}

is not a multiple of

\frac{π}{2}

, the lengths of

\vec{v}

and

\vec{u} \times \vec{v}

will not be the same and so the vector part will also end up being scaled between

|| \vec{v} ||

and

|| \vec{u} \times \vec{v} ||

.

This multiplication is equivalent to applying

e^{\vec{u} θ}

to both the

{\vec{v}}_{∥}

and

{\vec{v}}_{⊥}

parts:

e^{\vec{u} θ} \cdot \vec{v}

= e^{\vec{u} θ} \cdot ({\vec{v}}_{∥} + {\vec{v}}_{⊥})

= e^{\vec{u} θ} \cdot {\vec{v}}_{∥} + e^{\vec{u} θ} \cdot {\vec{v}}_{⊥}

= (\cos (θ), \sin (θ) \vec{u}) (0, {\vec{v}}_{∥}) + (\cos (θ), \sin (θ) \vec{u}) (0, {\vec{v}}_{⊥})

= (- \sin (θ) (\vec{u} \cdot {\vec{v}}_{∥}), \cos (θ) {\vec{v}}_{∥}) + (0, \cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥}))

= (- \sin (θ) (\vec{u} \cdot {\vec{v}}_{∥}), \cos (θ) \vec{v} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥}))

Note: \vec{u} \cdot \vec{v} = \vec{u} \cdot ({\vec{v}}_{∥} + {\vec{v}}_{⊥}) = \vec{u} \cdot {\vec{v}}_{∥} + 0 \Rightarrow - \sin (θ) (\vec{u} \cdot {\vec{v}}_{∥}) = - \sin (θ) (\vec{u} \cdot \vec{v})

Note: \vec{u} \times \vec{v} = \vec{u} \times ({\vec{v}}_{∥} + {\vec{v}}_{⊥}) = \vec{0} + \vec{u} \times {\vec{v}}_{⊥} \Rightarrow \sin (θ) (\vec{u} \times {\vec{v}}_{⊥}) = \sin (θ) (\vec{u} \times \vec{v})

= (- \sin (θ) (\vec{u} \cdot \vec{v}), \cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v}))

This shows that the multiplication

e^{\vec{u} θ} \cdot {\vec{v}}_{∥}

has side effects on

{\vec{v}}_{∥}

. For a valid 3D rotation,

{\vec{v}}_{∥}

should not be affected like this. Also note that the the multiplication

e^{\vec{u} θ} \cdot {\vec{v}}_{⊥}

produces

\cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})

, which is

{\vec{v}}_{⊥rot}

from Rodrigues' rotation formula. If these side effects can be removed from

{\vec{v}}_{∥}

, the product will be exactly the rotated vector from Rodrigues' rotation formula.

Note that we cannot apply

e^{\vec{u} θ}

to only

{\vec{v}}_{⊥}

because this equation only applies the rotation to the vector part of

\vec{v}

which is perpendicular to

\vec{u}

, and that operation cannot be converted to a single matrix vector multiplication. To build matrices which can be applied to any arbitrary 3D vector

\vec{v}

, the rotation must be applied to both

{\vec{v}}_{∥}

and

{\vec{v}}_{⊥}

:

e^{\vec{u} θ} \cdot {\vec{v}}_{∥} + e^{\vec{u} θ} \cdot {\vec{v}}_{⊥}

The side effects on

{\vec{v}}_{∥}

can be cancelled out by multiplying with the quaternion conjugate:

e^{\vec{u} θ} \cdot e^{- \vec{u} θ} \cdot {\vec{v}}_{∥}

= (1, 0) (0, {\vec{v}}_{∥})

= (0, {\vec{v}}_{∥})

= {\vec{v}}_{∥}

Note that this can also be accomplished by right multiplying with the conjugate:

e^{\vec{u} θ} \cdot {\vec{v}}_{∥} \cdot e^{- \vec{u} θ}

= (\cos (θ), \sin (θ) \vec{u}) (0, {\vec{v}}_{∥}) (\cos (θ), - \sin (θ) \vec{u})

= (- \sin (θ) (\vec{u} \cdot {\vec{v}}_{∥}), \cos (θ) {\vec{v}}_{∥} + \sin (θ) (\vec{u} \times {\vec{v}}_{∥})) (\cos (θ), - \sin (θ) \vec{u})

\vec{u} \times {\vec{v}}_{∥} = 0 since \vec{u} and {\vec{v}}_{∥} are parallel

= (- \sin (θ) (\vec{u} \cdot {\vec{v}}_{∥}), \cos (θ) {\vec{v}}_{∥}) (\cos (θ), - \sin (θ) \vec{u})

= (' - \sin (θ) \cos (θ) (\vec{u} \cdot {\vec{v}}_{∥}) + \sin (θ) \cos (θ) (\vec{u} \cdot {\vec{v}}_{∥}), \sin^{2} (θ) (\vec{u} \cdot {\vec{v}}_{∥}) \vec{u} + \cos^{2} (θ) {\vec{v}}_{∥} - \sin (θ) \cos (θ) ({\vec{v}}_{∥} \times \vec{u}))

Note: (\vec{u} \cdot {\vec{v}}_{∥}) \vec{u} = {\vec{v}}_{∥}

= (0, \sin^{2} (θ) {\vec{v}}_{∥} + \cos^{2} (θ) {\vec{v}}_{∥} - \sin (θ) \cos (θ) ({\vec{v}}_{∥} \times \vec{u}))

= (0, (\sin^{2} (θ) + \cos^{2} (θ)) {\vec{v}}_{∥} - \sin (θ) \cos (θ) ({\vec{v}}_{∥} \times \vec{u}))

Note: \sin^{2} (θ) + \cos^{2} (θ) = 1

Note: {\vec{v}}_{∥} \times \vec{u} = 0

= (0, {\vec{v}}_{∥})

= {\vec{v}}_{∥}

Also note what happens when

{\vec{v}}_{⊥}

is right multiplied by the conjugate:

e^{\vec{u} θ} \cdot {\vec{v}}_{⊥} \cdot e^{- \vec{u} θ}

= (\cos (θ), \sin (θ) \vec{u}) (0, {\vec{v}}_{⊥}) (\cos (θ), - \sin (θ) \vec{u})

= (- \sin (θ) (\vec{u} \cdot {\vec{v}}_{⊥}), \cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})) (\cos (θ), - \sin (θ) \vec{u})

\vec{u} \cdot {\vec{v}}_{⊥} = 0 since \vec{u} and {\vec{v}}_{⊥} are perpendicular

= (0, \cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})) (\cos (θ), - \sin (θ) \vec{u})

= (- \sin (θ) \vec{u} \cdot (\cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})), \cos (θ) (\cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})) + (\cos (θ) {\vec{v}}_{⊥} + \sin (θ) (\vec{u} \times {\vec{v}}_{⊥})) \times (- \sin (θ) \vec{u}))

= (- \sin (θ) \cos (θ) (\vec{u} \cdot {\vec{v}}_{⊥}) - \sin^{2} (θ) (\vec{u} \cdot (\vec{u} \times {\vec{v}}_{⊥})), \cos^{2} (θ) {\vec{v}}_{⊥} + \sin (θ) \cos (θ) (\vec{u} \times {\vec{v}}_{⊥}) - \sin (θ) \cos (θ) ({\vec{v}}_{⊥} \times \vec{u}) - \sin^{2} (θ) ((\vec{u} \times {\vec{v}}_{⊥}) \times \vec{u}))

\vec{u} \cdot {\vec{v}}_{⊥} = 0 since \vec{u} and {\vec{v}}_{⊥} are perpendicular

\vec{u} \cdot (\vec{u} \times {\vec{v}}_{⊥}) = 0 since \vec{u} and \vec{u} \times {\vec{v}}_{⊥} are perpendicular

\vec{u} \times {\vec{v}}_{⊥} = - {\vec{v}}_{⊥} \times \vec{u} by definition of the cross product

(\vec{u} \times {\vec{v}}_{⊥}) \times \vec{u} = - (\vec{u} \cdot {\vec{v}}_{⊥}) \vec{u} + (\vec{u} \cdot \vec{u}) {\vec{v}}_{⊥} by the triple product formula

= (0, \cos^{2} (θ) {\vec{v}}_{⊥} + 2 \sin (θ) \cos (θ) (\vec{u} \times {\vec{v}}_{⊥}) - \sin^{2} (θ) (- (\vec{u} \cdot {\vec{v}}_{⊥}) \vec{u} + (\vec{u} \cdot \vec{u}) {\vec{v}}_{⊥}))

- (\vec{u} \cdot {\vec{v}}_{⊥}) \vec{u} = 0 since \vec{u} and {\vec{v}}_{⊥} are perpendicular

\vec{u} \cdot \vec{u} = {|| \vec{u} ||}^{2} = 1

= (0, \cos^{2} (θ) {\vec{v}}_{⊥} + 2 \sin (θ) \cos (θ) (\vec{u} \times {\vec{v}}_{⊥}) - \sin^{2} (θ) {\vec{v}}_{⊥})

= (0, (\cos^{2} (θ) - \sin^{2} (θ)) {\vec{v}}_{⊥} + 2 \sin (θ) \cos (θ) (\vec{u} \times {\vec{v}}_{⊥}))

\cos^{2} (θ) - \sin^{2} (θ) = \cos (2 θ)

2 \sin (θ) \cos (θ) = \sin (2 θ)

= (0, \cos (2 θ) {\vec{v}}_{⊥} + \sin (2 θ) (\vec{u} \times {\vec{v}}_{⊥}))

This means the operation

e^{\vec{u} θ} \cdot \vec{v} \cdot e^{- \vec{u} θ}

does not change

{\vec{v}}_{∥}

, but it does rotate

{\vec{v}}_{⊥}

to compute

{\vec{v}}_{⊥rot}

, which gives the final result:

e^{\vec{u} θ} \cdot \vec{v} \cdot e^{- \vec{u} θ}

= e^{\vec{u} θ} \cdot ({\vec{v}}_{∥} + {\vec{v}}_{⊥}) \cdot e^{- \vec{u} θ}

= e^{\vec{u} θ} \cdot {\vec{v}}_{∥} \cdot e^{- \vec{u} θ} + e^{\vec{u} θ} \cdot {\vec{v}}_{⊥} \cdot e^{- \vec{u} θ}

= {\vec{v}}_{∥} + \cos (2 θ) {\vec{v}}_{⊥} + \sin (2 θ) (\vec{u} \times {\vec{v}}_{⊥})

In other words,

{\vec{v}}_{∥}

remains the same, and

{\vec{v}}_{⊥}

gets rotated by

2 θ

around

\vec{u}

. This is exactly Rodrigues' rotation formula, but with the angle of rotation doubled. This can be worked around by simply dividing the angle of rotation by two,

e^{\vec{u} \frac{θ}{2}}

.

Converting quaternions to matrices:

The operation

e^{\vec{u} θ} \cdot \vec{v} \cdot e^{- \vec{u} θ}

can be converted into a matrix multiplication by factoring out

\vec{v}

:

e^{\vec{u} θ} \cdot \vec{v} \cdot e^{- \vec{u} θ}

= (\cos (θ), \sin (θ) \vec{u}) \cdot (0, \vec{v}) \cdot (\cos (θ), - \sin (θ) \vec{u})

= (- \sin (θ) (\vec{u} \cdot \vec{v}), \cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v})) \cdot (\cos (θ), - \sin (θ) \vec{u})

The scalar part of the product becomes:

- \sin (θ) \cos (θ) (\vec{u} \cdot \vec{v}) - (\cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v})) \cdot (- \sin (θ) \vec{u})

= - \sin (θ) \cos (θ) (\vec{u} \cdot \vec{v}) + \sin (θ) \cos (θ) (\vec{u} \cdot \vec{v}) + \sin^{2} (θ) (\vec{u} \cdot (\vec{u} \times \vec{v}))

= \sin^{2} (θ) (\vec{u} \cdot (\vec{u} \times \vec{v}))

\vec{u} \cdot (\vec{u} \times \vec{v}) = 0 since \vec{u} and \vec{u} \times \vec{v} are perpendicular

= 0

The vector part of the product becomes:

\sin^{2} (θ) (\vec{u} \cdot \vec{v}) \vec{u} + \cos (θ) (\cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v})) + (\cos (θ) \vec{v} + \sin (θ) (\vec{u} \times \vec{v})) \times (- \sin (θ) \vec{u})

= \sin^{2} (θ) (\vec{u} \cdot \vec{v}) \vec{u} + \cos^{2} (θ) \vec{v} + \sin (θ) \cos (θ) (\vec{u} \times \vec{v}) - \sin (θ) \cos (θ) (\vec{v} \times \vec{u}) - \sin^{2} (θ) ((\vec{u} \times \vec{v}) \times \vec{u})

(\vec{u} \times \vec{v}) \times \vec{u} = - (\vec{u} \cdot \vec{v}) \vec{u} + (\vec{u} \cdot \vec{u}) \vec{v} by the triple product formula

= \sin^{2} (θ) (\vec{u} \cdot \vec{v}) \vec{u} + \cos^{2} (θ) \vec{v} + 2 \sin (θ) \cos (θ) (\vec{u} \times \vec{v}) - \sin^{2} (θ) (- (\vec{u} \cdot \vec{v}) \vec{u} + (\vec{u} \cdot \vec{u}) \vec{v})

(\vec{u} \cdot \vec{u}) \vec{v} = {|| \vec{u} ||}^{2} \vec{v} = \vec{v}

= \sin^{2} (θ) (\vec{u} \cdot \vec{v}) \vec{u} + \cos^{2} (θ) \vec{v} + 2 \sin (θ) \cos (θ) (\vec{u} \times \vec{v}) + \sin^{2} (θ) (\vec{u} \cdot \vec{v}) \vec{u} - \sin^{2} (θ) \vec{v}

= 2 \sin^{2} (θ) (\vec{u} \cdot \vec{v}) \vec{u} + (\cos^{2} (θ) - \sin^{2} (θ)) \vec{v} + 2 \sin (θ) \cos (θ) (\vec{u} \times \vec{v})

\sin^{2} (θ) = \frac{1 - \cos (2 θ)}{2}

\cos^{2} (θ) - \sin^{2} (θ) = \cos (2 θ)

2 \sin (θ) \cos (θ) = \sin (2 θ)

= (1 - \cos (2 θ)) (\vec{u} \cdot \vec{v}) \vec{u} + \cos (2 θ) \vec{v} + \sin (2 θ) (\vec{u} \times \vec{v})

This has just become Rodrigues' rotation formula. As shown previously, this can be converted directly into the matrix-vector multiplication:

[\begin{matrix} \cos (2 θ) + (1 - \cos (2 θ)) {u_{x}}^{2} & - \sin (2 θ) u_{z} + (1 - \cos (2 θ)) u_{x} u_{y} & \sin (2 θ) u_{y} + (1 - \cos (2 θ)) u_{x} u_{z} \\ \sin (2 θ) u_{z} + (1 - \cos (2 θ)) u_{x} u_{y} & \cos (2 θ) + (1 - \cos (2 θ)) {u_{y}}^{2} & - \sin (2 θ) u_{x} + (1 - \cos (2 θ)) u_{y} u_{z} \\ - \sin (2 θ) u_{y} + (1 - \cos (2 θ)) u_{x} u_{z} & \sin (2 θ) u_{x} + (1 - \cos (2 θ)) u_{y} u_{z} & \cos (2 θ) + (1 - \cos (2 θ)) {u_{z}}^{2} \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}]

This rotation matrix can be generated directly from a given quaternion

q = a + b i + c j + d k = \cos (θ) + \sin (θ) u_{x} i + \sin (θ) u_{y} j + \sin (θ) u_{z} k = e^{\vec{u} θ}

with the following substitutions using trigonometric identities:

[\begin{matrix} (2 a^{2} - 1) + 2 b^{2} & - 2 a d + 2 b c & 2 a c + 2 b d \\ 2 a d + 2 b c & (2 a^{2} - 1) + 2 c^{2} & - 2 a b + 2 c d \\ - 2 a c + 2 b d & 2 a b + 2 c d & (2 a^{2} - 1) + 2 d^{2} \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}]

Then simplifying a bit more with factoring and the fact that

a^{2} + b^{2} + c^{2} + d^{2} = 1

:

[\begin{matrix} 1 - 2 (c^{2} + d^{2}) & 2 (b c - a d) & 2 (a c + b d) \\ 2 (a d + b c) & 1 - 2 (b^{2} + d^{2}) & 2 (c d - a b) \\ 2 (b d - a c) & 2 (a b + c d) & 1 - 2 (b^{2} + c^{2}) \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}]

Euler angle's to quaternions:

A quaternion can be created from Euler angles as follows.

First construct a quaternion for each axis:

q_{x} = (\cos (θ_{x}), \sin (θ_{x}) (1 i + 0 j + 0 k)) = (\cos (θ_{x}), \sin (θ_{x}) i)

q_{y} = (\cos (θ_{y}), \sin (θ_{y}) (0 i + 1 j + 0 k)) = (\cos (θ_{y}), \sin (θ_{y}) j)

q_{z} = (\cos (θ_{z}), \sin (θ_{z}) (0 i + 0 j + 1 k)) = (\cos (θ_{z}), \sin (θ_{z}) k)

Then combine them all to form the combined quaternion:

q_{x} q_{y} q_{z}

= (\cos (θ_{x}), \sin (θ_{x}) i) (\cos (θ_{y}), \sin (θ_{y}) j) (\cos (θ_{z}), \sin (θ_{z}) k)

= (\cos (θ_{x}) \cos (θ_{y}) - \sin (θ_{x}) \sin (θ_{y}) (i \cdot j), \sin (θ_{x}) \cos (θ_{y}) i + \sin (θ_{y}) \cos (θ_{x}) j + \sin (θ_{x}) \sin (θ_{y}) (i \times j)) (\cos (θ_{z}), \sin (θ_{z}) k)

= (\cos (θ_{x}) \cos (θ_{y}), \sin (θ_{x}) \cos (θ_{y}) i + \sin (θ_{y}) \cos (θ_{x}) j + \sin (θ_{x}) \sin (θ_{y}) k) (\cos (θ_{z}), \sin (θ_{z}) k)

= \cos (θ_{x}) \cos (θ_{y}) \cos (θ_{z}) - (\sin (θ_{x}) \cos (θ_{y}) i + \sin (θ_{y}) \cos (θ_{x}) j + \sin (θ_{x}) \sin (θ_{y}) k) \cdot \sin (θ_{z}) k

+ \cos (θ_{z}) (\sin (θ_{x}) \cos (θ_{y}) i + \sin (θ_{y}) \cos (θ_{x}) j + \sin (θ_{x}) \sin (θ_{y}) k) + \cos (θ_{x}) \cos (θ_{y}) \sin (θ_{z}) k

+ (\sin (θ_{x}) \cos (θ_{y}) i + \sin (θ_{y}) \cos (θ_{x}) j + \sin (θ_{x}) \sin (θ_{y}) k) \times \sin (θ_{z}) k

= \cos (θ_{x}) \cos (θ_{y}) \cos (θ_{z}) - \sin (θ_{x}) \sin (θ_{y}) \sin (θ_{z})

+ \sin (θ_{x}) \cos (θ_{y}) \cos (θ_{z}) i + \cos (θ_{x}) \sin (θ_{y}) \cos (θ_{z}) j + \sin (θ_{x}) \sin (θ_{y}) \cos (θ_{z}) k + \cos (θ_{x}) \cos (θ_{y}) \sin (θ_{z}) k

- \sin (θ_{x}) \cos (θ_{y}) \sin (θ_{z}) j + \sin (θ_{y}) \cos (θ_{x}) \sin (θ_{z}) i

= \cos (θ_{x}) \cos (θ_{y}) \cos (θ_{z}) - \sin (θ_{x}) \sin (θ_{y}) \sin (θ_{z})

+ (\sin (θ_{x}) \cos (θ_{y}) \cos (θ_{z}) + \cos (θ_{x}) \sin (θ_{y}) \sin (θ_{z})) i

+ (\cos (θ_{x}) \sin (θ_{y}) \cos (θ_{z}) - \sin (θ_{x}) \cos (θ_{y}) \sin (θ_{z})) j

+ (\sin (θ_{x}) \sin (θ_{y}) \cos (θ_{z}) + \cos (θ_{x}) \cos (θ_{y}) \sin (θ_{z})) k

Quaternion to axis angle:

Let

q = (\cos (\frac{θ}{2}), \sin (\frac{θ}{2}) \vec{u})

be the quaternion used to represent a rotation of

θ

radians around the axis

\vec{u}

.

The angle of rotation

θ

can be read from the scalar component

q_{s} = \cos (\frac{θ}{2})

:

θ = 2 \arccos (q_{s})

The axis of rotation

\vec{u}

can be obtained by normalizing the vector component

q_{\vec{v}} = \sin (\frac{θ}{2}) \vec{u}

:

\frac{q_{\vec{v}}}{|| q_{\vec{v}} ||}

= \frac{\sin (\frac{θ}{2}) \vec{u}}{|| \sin (\frac{θ}{2}) \vec{u} ||}

= \vec{u}

Rotation matrix to quaternion:

Let

R

be the rotation matrix generated from the quaternion

q = (\cos (θ), \sin (θ) \vec{u})

:

R = [\begin{matrix} 1 - 2 (c^{2} + d^{2}) & 2 (b c - a d) & 2 (a c + b d) \\ 2 (a d + b c) & 1 - 2 (b^{2} + d^{2}) & 2 (c d - a b) \\ 2 (b d - a c) & 2 (a b + c d) & 1 - 2 (b^{2} + c^{2}) \end{matrix}]

The quaternion can be read from the matrix as follows:

R_{11} + R_{22} + R_{33}

= (1 - 2 (c^{2} + d^{2})) + (1 - 2 (b^{2} + d^{2})) + (1 - 2 (b^{2} + c^{2}))

= 3 - 4 (b^{2} + c^{2} + d^{2})

Note: a^{2} + b^{2} + c^{2} + d^{2} = 1 \Rightarrow b^{2} + c^{2} + d^{2} = 1 - a^{2} since q is a unit quaternion

= 3 - 4 (1 - a^{2})

= 4 a^{2} - 1

\Rightarrow \sqrt{\frac{R_{11} + R_{22} + R_{33} + 1}{4}} = \frac{1}{2} \sqrt{R_{11} + R_{22} + R_{33} + 1} = a

\Rightarrow \frac{R_{23} - R_{32}}{4 a} = \frac{2 (a b + c d) - 2 (c d - a b)}{4 a} = \frac{4 a b}{4 a} = b

\Rightarrow \frac{R_{31} - R_{13}}{4 a} = \frac{2 (a c + b d) - 2 (b d - a c)}{4 a} = \frac{4 a c}{4 a} = c

\Rightarrow \frac{R_{12} - R_{21}}{4 a} = \frac{2 (a d + b c) - 2 (b c - a d)}{4 a} = \frac{4 a d}{4 a} = d

This only works if

a

is greater than zero. These are the other equivalent calculations if

a

is zero:

R_{11} - R_{22} - R_{33}

= (1 - 2 (c^{2} + d^{2})) - (1 - 2 (b^{2} + d^{2})) - (1 - 2 (b^{2} + c^{2}))

= 4 b^{2} - 1

\Rightarrow \sqrt{\frac{R_{11} - R_{22} - R_{33} + 1}{4}} = \frac{1}{2} \sqrt{R_{11} - R_{22} - R_{33} + 1} = b

\Rightarrow \frac{R_{23} - R_{32}}{4 b} = \frac{2 (a b + c d) - 2 (c d - a b)}{4 b} = \frac{4 a b}{4 b} = a

\Rightarrow \frac{R_{12} + R_{21}}{4 b} = \frac{2 (a d + b c) + 2 (b c - a d)}{4 b} = \frac{4 b c}{4 b} = c

\Rightarrow \frac{R_{31} + R_{13}}{4 b} = \frac{2 (a c + b d) + 2 (b d - a c)}{4 b} = \frac{4 b d}{4 b} = d

- R_{11} + R_{22} - R_{33}

= - (1 - 2 (c^{2} + d^{2})) + (1 - 2 (b^{2} + d^{2})) - (1 - 2 (b^{2} + c^{2}))

= 4 c^{2} - 1

\Rightarrow \sqrt{\frac{- R_{11} + R_{22} - R_{33} + 1}{4}} = \frac{1}{2} \sqrt{- R_{11} + R_{22} - R_{33} + 1} = c

\Rightarrow \frac{R_{31} - R_{13}}{4 c} = \frac{2 (a c + b d) - 2 (b d - a c)}{4 c} = \frac{4 a c}{4 c} = a

\Rightarrow \frac{R_{12} + R_{21}}{4 c} = \frac{2 (a d + b c) + 2 (b c - a d)}{4 c} = \frac{4 b c}{4 c} = b

\Rightarrow \frac{R_{23} + R_{32}}{4 c} = \frac{2 (a b + c d) + 2 (c d - a b)}{4 c} = \frac{4 c d}{4 c} = d

- R_{11} - R_{22} + R_{33}

= - (1 - 2 (c^{2} + d^{2})) - (1 - 2 (b^{2} + d^{2})) + (1 - 2 (b^{2} + c^{2}))

= 4 d^{2} - 1

\Rightarrow \sqrt{\frac{- R_{11} - R_{22} + R_{33} + 1}{4}} = \frac{1}{2} \sqrt{- R_{11} - R_{22} + R_{33} + 1} = d

\Rightarrow \frac{R_{12} - R_{21}}{4 d} = \frac{2 (a d + b c) - 2 (b c - a d)}{4 d} = \frac{4 a d}{4 d} = a

\Rightarrow \frac{R_{31} + R_{13}}{4 d} = \frac{2 (a c + b d) + 2 (b d - a c)}{4 d} = \frac{4 b d}{4 d} = b

\Rightarrow \frac{R_{23} + R_{32}}{4 d} = \frac{2 (a b + c d) + 2 (c d - a b)}{4 d} = \frac{4 c d}{4 d} = c

Sources:

Euclidean Space - Conversion Matrix to Quaternion: https://www.euclideanspace.com/maths/geometry/rotations/conversions/matrixToQuaternion/
Khan Academy - Maclaurin series of cos(x): https://www.khanacademy.org/math/ap-calculus-bc/bc-series-new/bc-10-14/v/cosine-taylor-series-at-0-maclaurin
Khan Academy - Maclaurin series of sin(x): https://www.khanacademy.org/math/ap-calculus-bc/bc-series-new/bc-10-14/v/sine-taylor-series-at-0-maclaurin
Khan Academy - Maclaurin series of e^x: https://www.khanacademy.org/math/ap-calculus-bc/bc-series-new/bc-10-14/v/taylor-series-at-0-maclaurin-for-e-to-the-x
Khan Academy - Euler's formula & Euler's identity: https://www.khanacademy.org/math/ap-calculus-bc/bc-series-new/bc-10-14/v/euler-s-formula-and-euler-s-identity
Wikipedia - Complex numbers: https://en.wikipedia.org/wiki/Complex_number
Wikipedia - Polar coordinates: https://en.wikipedia.org/wiki/Polar_coordinate_system
Wikipedia - Quaternions: https://en.wikipedia.org/wiki/Quaternion
Wikipedia - Quaternions and spatial rotation: https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation
Wikipedia - Rodrigues' rotation formula: https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
Youtube - 3Blue1Browns's video "Quaternions and 3d rotation, explained interactively": https://youtu.be/zjMuIxRvygQ
Youtube - 3Blue1Browns's video "Visualizing quaternions (4d numbers) with stereographic projection": https://youtu.be/d4EgbgTm0Bg
Youtube - Mathoma's video "3D Rotations in General: Rodrigues Rotation Formula and Quaternion Exponentials": https://youtu.be/q-ESzg03mQc
Youtube - Mathoma's video "3D Rotations and Quaternion Exponentials: Special Case": https://youtu.be/UaK2q22mMEg
Youtube - Mathoma's video "Euler's Formula for the Quaternions": https://youtu.be/88BA8aO3qXA
Youtube - Mathoma's video "Quaternions as 4x4 Matrices - Connections to Linear Algebra": https://youtu.be/3Ki14CsP_9k
Youtube - Mathoma's video "Quaternions EXPLAINED Briefly": https://youtu.be/jlskQDR8-bY